In
the previous section we have seen that fst
can take different values. To explain this behaviour, we will discuss
about the stages that lead to the failure of a beam section.
Consider a beam being loaded. When the load increases, the stresses in concrete and steel also increase. The internal moment which resist the applied external bending moment is given by Force x Lever arm. This is shown in the fig. below:
Fig.3.21
Internal moment at the beam section
The force that we use for computation of the internal moment can be the compressive force C in concrete or the tensile force T in steel. Both will give the same result. So we can write:
Internal moment developed = T x z = C x z
z is the lever arm, which is the distance between the point of application of C and T. C acts at the centroid of the concrete stress block and T acts at the centroid of steel.
Let us now see the different stages that the beam section will pass through, while it is being loaded to the ultimate state:
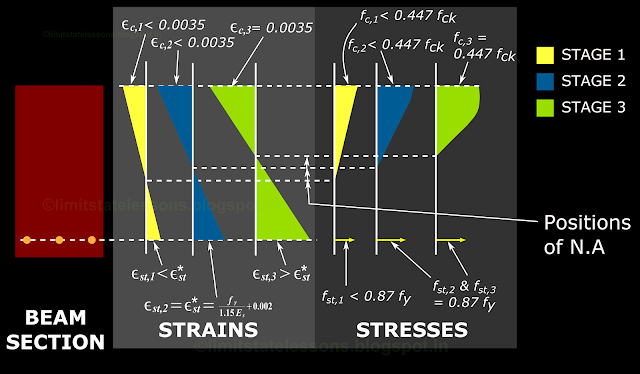
Stage 1: C and T increases normally to resist the external load. The stresses and strains are in the linear elastic state. This is shown in the fig.3.22 below. The strain in steel at this stage is denoted as εst,1. This is less than ε*st .
Here ε*st is the 'quantity of strain' which when obtained, confirmation can be made that the steel has yielded. This is the last point of the curved portion, which is obtained by drawing the dashed parallel line through 0.002 strain. (The last row in the table for Fe415 and Fe500) So we can write:
Eq.3.12
In the stage 1, εst,1 < ε*st , because the steel has not yielded. It is in the initial linear elastic state. Also εc,1 the strain in concrete is far less than 0.0035, the ultimate strain. The stress fst,1 in steel is less than 0.87fy . We know that 0.87fy is the design yield stress (fy/1.15 = 0.87fy). That is., the stress corresponding to the strain ε*st.
The stress fc,1 in the top most compression fibre is far less than 0.447fck , the ultimate stress in concrete.
Fig.3.22
Stages before failure of beam section
Stage 2: The steel enters the non-linear stage and has begun to yield. But once the steel has yielded, it will continue to elongate at constant stress. That is., the strain will increase at constant stress. (The final horizontal line of the stress-strain curve). As the stress in steel is constant, the force T in it is also constant. But as the external load is being increased, the applied bending- moment is also increasing.
As T is remaining constant, the resisting internal moment can be increased only by increasing z. 'z' is the distance between the centroid of concrete stress block and the centroid of steel. The centroid of steel cannot change as it is held in position. But centroid of concrete stress block can change. For this, the effective concrete area taking part in the compression should decrease. For this, the NA should move upwards. Then, the total height of the concrete stress block will decrease, and it's centroid will move upwards. When this happens, the lever-arm z will increase.
These details can be seen in the fig.3.22 above. In the stage 2, the strain εst,2 in steel has become equal to ε*st . So the steel has yielded. The NA has shifted upwards. The strain εc,2 in the top most compression fibre is still less than 0.0035.
The stress fst,2 in steel is at the constant value of 0.87fy. The stress in concrete fc,2 is less than 0.447fck.
So even though the steel has yielded, the section manages to resist the external bending-moment by increasing z. But as part of the experiment, we are increasing the load further. So the beam moves on to the next stage.
Stage 3: The reduced area of concrete has to take more load now. As a result, stress in it begins to increase. The strain also increase. But the concrete cannot take large strains as in the case of steel.
We have seen the difference in the strain values of concrete and steel (fig.2.15) when we discussed the working stress method. Here also in the limit state method, this difference in strains has much significance. So we will write it down again:
The reinforcing steel have a greater ductility. It can undergo greater strains than concrete. Yielding of steel occurs at higher stresses, and the amount of yield, which is measured as strain can be in the range 0.12 to 0.20, before failure of steel occur. But for concrete, this range is 0.003 to 0.0045. To get a better understanding of these ranges, we can think of two specimens, one of concrete and the other of steel. Let both of them have the same length of say 20 cm, then the maximum increase in length that the steel specimen can have is calculated as follows:
Strain = Δl / l = 0.12 to 0.20. So Δl = 0.12 x 20 to 0.2 x 20cm = 2.4 to 4.0cm
Similarly, the decrease in length that the concrete specimen can have is calculated as follows:
Strain = Δl / l = 0.003 to 0.0045. So Δl = 0.003 x 20 to 0.0045 x 20cm = 0.06 to 0.09cm
From the above, we can see that, when concrete and steel are combined to form a composite material, at higher stresses, the concrete will fail before failure of steel occurs. This happens in our beam also: The load is being increased even after the yielding of steel has occured. Concrete cannot take this large strain, and it will soon reach the ultimate strain of 0.0035, and will fail by crushing.
But before this failure of concrete occur, the steel has yielded to a greater extent. This cause the beam to deflect more and the cracks at the bottom side of the beam become wider. Such deflections and wider cracks give sufficient warning about the beam failure that is about to take place.
So the failure of the beam is by the crushing of concrete. But it was initiated by the yielding of steel under tension. This type of failure is called tension failure.
The details of stage 3 are shown in the fig.3.22 above In the stage 3, the strain εst,3 in steel has become greater than ε*st . This is because the steel is elongating at constant stress. The NA has shifted further upwards. The strain εc,3 in the top most compression fibre has reached 0.0035, which is the ultimate strain.
The stress fst,3 in steel is at the constant value of 0.87fy. The stress in concrete fc,3 has reached 0.447fck.
It may be noted that in the above experiment, we say that the beam has reached the ultimate state (the state of impending failure), when the strain in the top most compression fibre reached 0.0035. The steel began to yield long before this strain was obtained in concrete. But yielding of steel cannot be taken as a criterion for reaching the ultimate state. Because, as stated earlier, steel can continue to perform through larger strains. The concrete cannot go through these larger strains and so will fail before steel. The beam will serve it's purpose only if both steel and concrete are performing satisfactorily at all the sections. But here concrete has reached it's ultimate state. So the beam as a whole has reached it's ultimate state. Thus strain value of 0.0035 in the extreme compression fibre of concrete is taken as the criterion for deciding whether the beam has reached ultimate state or not.
The beam shown in fig.3.19 of the previous section is an example of this type of beam. In it, the stress and strain in steel at the ultimate state is in the magenta colored straight line region. So the steel has yielded.
Suppose in the experiment, the beam that we used, has a larger area of steel and/or the steel is of high strength grade, then the results would be different. In the next section we will see the details of such a beam.
PREVIOUS
NEXT
Consider a beam being loaded. When the load increases, the stresses in concrete and steel also increase. The internal moment which resist the applied external bending moment is given by Force x Lever arm. This is shown in the fig. below:
Fig.3.21
Internal moment at the beam section
The force that we use for computation of the internal moment can be the compressive force C in concrete or the tensile force T in steel. Both will give the same result. So we can write:
Internal moment developed = T x z = C x z
z is the lever arm, which is the distance between the point of application of C and T. C acts at the centroid of the concrete stress block and T acts at the centroid of steel.
Let us now see the different stages that the beam section will pass through, while it is being loaded to the ultimate state:
Stage 1: C and T increases normally to resist the external load. The stresses and strains are in the linear elastic state. This is shown in the fig.3.22 below. The strain in steel at this stage is denoted as εst,1. This is less than ε*st .
Here ε*st is the 'quantity of strain' which when obtained, confirmation can be made that the steel has yielded. This is the last point of the curved portion, which is obtained by drawing the dashed parallel line through 0.002 strain. (The last row in the table for Fe415 and Fe500) So we can write:
Eq.3.12
In the stage 1, εst,1 < ε*st , because the steel has not yielded. It is in the initial linear elastic state. Also εc,1 the strain in concrete is far less than 0.0035, the ultimate strain. The stress fst,1 in steel is less than 0.87fy . We know that 0.87fy is the design yield stress (fy/1.15 = 0.87fy). That is., the stress corresponding to the strain ε*st.
The stress fc,1 in the top most compression fibre is far less than 0.447fck , the ultimate stress in concrete.
Fig.3.22
Stages before failure of beam section
Stage 2: The steel enters the non-linear stage and has begun to yield. But once the steel has yielded, it will continue to elongate at constant stress. That is., the strain will increase at constant stress. (The final horizontal line of the stress-strain curve). As the stress in steel is constant, the force T in it is also constant. But as the external load is being increased, the applied bending- moment is also increasing.
As T is remaining constant, the resisting internal moment can be increased only by increasing z. 'z' is the distance between the centroid of concrete stress block and the centroid of steel. The centroid of steel cannot change as it is held in position. But centroid of concrete stress block can change. For this, the effective concrete area taking part in the compression should decrease. For this, the NA should move upwards. Then, the total height of the concrete stress block will decrease, and it's centroid will move upwards. When this happens, the lever-arm z will increase.
These details can be seen in the fig.3.22 above. In the stage 2, the strain εst,2 in steel has become equal to ε*st . So the steel has yielded. The NA has shifted upwards. The strain εc,2 in the top most compression fibre is still less than 0.0035.
The stress fst,2 in steel is at the constant value of 0.87fy. The stress in concrete fc,2 is less than 0.447fck.
So even though the steel has yielded, the section manages to resist the external bending-moment by increasing z. But as part of the experiment, we are increasing the load further. So the beam moves on to the next stage.
Stage 3: The reduced area of concrete has to take more load now. As a result, stress in it begins to increase. The strain also increase. But the concrete cannot take large strains as in the case of steel.
We have seen the difference in the strain values of concrete and steel (fig.2.15) when we discussed the working stress method. Here also in the limit state method, this difference in strains has much significance. So we will write it down again:
The reinforcing steel have a greater ductility. It can undergo greater strains than concrete. Yielding of steel occurs at higher stresses, and the amount of yield, which is measured as strain can be in the range 0.12 to 0.20, before failure of steel occur. But for concrete, this range is 0.003 to 0.0045. To get a better understanding of these ranges, we can think of two specimens, one of concrete and the other of steel. Let both of them have the same length of say 20 cm, then the maximum increase in length that the steel specimen can have is calculated as follows:
Strain = Δl / l = 0.12 to 0.20. So Δl = 0.12 x 20 to 0.2 x 20cm = 2.4 to 4.0cm
Similarly, the decrease in length that the concrete specimen can have is calculated as follows:
Strain = Δl / l = 0.003 to 0.0045. So Δl = 0.003 x 20 to 0.0045 x 20cm = 0.06 to 0.09cm
From the above, we can see that, when concrete and steel are combined to form a composite material, at higher stresses, the concrete will fail before failure of steel occurs. This happens in our beam also: The load is being increased even after the yielding of steel has occured. Concrete cannot take this large strain, and it will soon reach the ultimate strain of 0.0035, and will fail by crushing.
But before this failure of concrete occur, the steel has yielded to a greater extent. This cause the beam to deflect more and the cracks at the bottom side of the beam become wider. Such deflections and wider cracks give sufficient warning about the beam failure that is about to take place.
So the failure of the beam is by the crushing of concrete. But it was initiated by the yielding of steel under tension. This type of failure is called tension failure.
The details of stage 3 are shown in the fig.3.22 above In the stage 3, the strain εst,3 in steel has become greater than ε*st . This is because the steel is elongating at constant stress. The NA has shifted further upwards. The strain εc,3 in the top most compression fibre has reached 0.0035, which is the ultimate strain.
The stress fst,3 in steel is at the constant value of 0.87fy. The stress in concrete fc,3 has reached 0.447fck.
It may be noted that in the above experiment, we say that the beam has reached the ultimate state (the state of impending failure), when the strain in the top most compression fibre reached 0.0035. The steel began to yield long before this strain was obtained in concrete. But yielding of steel cannot be taken as a criterion for reaching the ultimate state. Because, as stated earlier, steel can continue to perform through larger strains. The concrete cannot go through these larger strains and so will fail before steel. The beam will serve it's purpose only if both steel and concrete are performing satisfactorily at all the sections. But here concrete has reached it's ultimate state. So the beam as a whole has reached it's ultimate state. Thus strain value of 0.0035 in the extreme compression fibre of concrete is taken as the criterion for deciding whether the beam has reached ultimate state or not.
The beam shown in fig.3.19 of the previous section is an example of this type of beam. In it, the stress and strain in steel at the ultimate state is in the magenta colored straight line region. So the steel has yielded.
Suppose in the experiment, the beam that we used, has a larger area of steel and/or the steel is of high strength grade, then the results would be different. In the next section we will see the details of such a beam.
PREVIOUS
NEXT
Copyright ©2015 limitstatelessons.blogspot.com - All Rights Reserved

No comments:
Post a Comment