Chapter 2 (cont..1)

In the previous section, we saw the ‘Cracking moment’, which is the bending moment at which the beam section will crack at the tension side for the first time. Now we can discuss about the stages after cracking. At the end of the previous section, what we saw was the uncracked phase of the beam. This phase comes to an end when the load increases and the moment applied on the beam reaches M_cr. Now the next phase begins and it is called the Linear Elastic Cracked Phase. In this phase cracks begin to appear at the bottom most fibres of the concrete. As the load increases, these cracks widens and propagates upwards towards the neutral axis. The term 'Linear elastic' is used in the name of this phase because the stress is proportional to strain in both concrete and steel, and they can be represented by straight lines. Also the elongation of steel and the compression of concrete are ‘elastic’ in nature. That is., if we release the load, the materials will regain their original dimensions. Just as we obtained the value of M_cr and the corresponding stress, the modulus of rupture  f_cr which mark the end of phase 1, we will now obtain the values which mark the end of phase 2.

When the concrete has cracked, it will not take any tension. So the tension is now taken up entirely by the steel. Let us assume that the load which is being increased gradually, has reached the level corresponding to the end of phase 2. We will stop the loading here for a while to derive the expressions for various quantities. Fig 2.10 below shows the comparison of the sections before and after cracking.

Fig.2.10
Comparison between Uncracked and cracked sections

The concrete below the neutral axis is cracked and it is shown as a hollow region in fig 2.10(c). So there is a loss of material below NA. Because of this loss of material, the NA shifts upwards, or in other words the depth of NA decreases. This can be seen from the higher level of NA in figs.2.10 (c) and (d). The NA now passes through the centroid of the new transformed section. At this stage, all the tensile force is taken up by the reinforcing steel of area A_st. Concrete does not take any tensile force. Fig 2.11 below shows the stress distribution and the commonly used notations for the analysis in this phase.

Fig.2.11
Stress distribution in a cracked section

From the fig, we can see that the depth of neutral axis is expressed as kd where k is a fraction. So the depth of NA is expressed as a fraction of effective depth d.

In the above fig.2.11, kd, jd, f_c etc., are the notations of quantities, for which we are going to derive expressions in our discussions. f_st is also such a notation. But ‘f_st /m’ is derived after some calculations which are already done:

We are having a transformed section in which all the steel has been removed. The steel is replaced by concrete of area mA_st . So at the level of steel in the stress diagram, we will be obtaining the stress  f_cs in concrete. But we are interested in the stress in steel. So we use Eq.2.13 which we derived in the previous section, by which, the stress in Material 2 (steel) is m times the stress in Material 1 (concrete). So we rearrange the equation in such a way as to bring f_st into the picture. Thus we write ‘f_st /m’ in place of f_cs 

Moment of the top compression area about the NA is
 Moment of the bottom tension area about NA is
mA_st(d-kd)

Equating the above two we get

Eq.2.15
 = 0

This is a quadratic equation in k and can be easily solved. We have seen that k is a fraction. So out of the two solutions, the value which is ‘positive’ and at the same time ‘less than one’ should be taken.

The Moment of Inertia of the cracked section denoted by I_cr can be calculated using elementary mechanics and is given by:

Eq.2.16

From Eq.2.15, we will get the position of the NA, and from Eq.2.16, we will get I_cr. Now, the only unknowns remaining in fig.2.11 are f_c and f_st . For calculating them, we take the basic bending equation:

From this, we get the expression for f_c as:

Eq.2.17

and the expression for f_st as:

Eq.2.18

Another method for obtaining f_c and f_st is as follows:

In fig 2.11, the area of the upper triangle is 0.5f_ckd The total compressive force is equal to the volume of the upper stress block, which is obtained by multiplying the area of the triangle with the width b of the section.So compressive force C is obtained as

Eq.2.19
C =0.5b kd f_c

This force acts at the centroid of the upper stress block, which is at a distance of kd/3  from the top most fibre.

Now consider the tensile force. The tensile force T  in the steel is obtained by multiplying the stress in steel by the area of steel.

Eq.2.20
T =A_st f_st

The external moment is equal to the resisting moment offered by the section, and is obtained by multiplying the force with the lever arm jd. Thus:

Eq.2.21 and 2.22
M =C jd  and M =T jd

Substituting 2.19 in 2.21 we get

Eq.2.23
M =0.5b f_c (kd)(jd)

Substituting 2.20 in 2.22 we get

Eq.2.24
M =A_st f_st (jd)

From 2.23 we get

Eq.2.25

From 2.24 we get

Eq.2.26

Yet another method is as follows: Knowing f_c  , f_st  can be calculated by using similar triangles in fig. 2.11

Base of upper triangle = f_c . Base of lower triangle = f_st /m.
Altitude of upper triangle = kd . Altitude of lower triangle = d -kd. So:
 

Thus we get:

Eq.2.27

So we are now in the phase 2 and we derived the following:
• Equation to find the compressive stress in the extreme fibre in concrete and
• Equation to find the tensile stress in the steel.
Compare this with what we did in phase 1. In phase 1, we have an expression for the modulus of rupture  f_cr , which is given directly by the code. Using f_cr , we calculated the cracking moment. This cracking moment marks the end of phase 1 and the beginning of phase2.

The first crack of concrete marks the end of phase 1. So only concrete is involved. Steel does not come into the picture. But in phase 2, steel also takes the load, and we have the above expressions 2.17, 2.18, 2.25, 2.26 and 2.27 to find the stresses in concrete and steel. So now how do we mark the end of phase 2 ?

Just as f_c was limited to f_cr in phase 1, we have some limiting values in phase 2 also. They are as follows:
• f_c is limited to σ_cbc   given by table 21 of the code and
• f_st is limited to σ_st   given by table 22 of the code

σ_cbc is the permissible stress in concrete, obtained from table 21 of the code (discussed earlier in the case of modular ratio of reinforced concrete), and σ_st is the permissible stress in reinforcing steel. The values of σ_st can be obtained from table 22 of the code. These values are shown below in Table 2-2.

If σ_cbc is reached, the code assumes that the concrete has been compressed to the maximum value of allowable compressive stress, and the section has become unsafe. Similarly if σ_st is reached, the code assumes that steel has been stretched to the maximum allowable tensile stress, and the section has become unsafe.

So for any given load, we can calculate the corresponding Bending moment at any section. We can then calculate f_c and f_st , compare it with σ_cbc and σ_st , and then say whether it is safe or not. The ability to say whether a particular load is safe or not is not sufficient. We want to be able to ‘specify the load’ at which the beam will become unsafe. So that the loading can be stopped before reaching that particular value of load. In the following discussions, we will see how this can be done.

While loading a beam, if f_c attains the value σ_cbc , then we say that the end of phase 2 is reached. If f_st attains the value σ_st , then also we say that the end of phase 2 is reached. We can do some further analysis to determine which of the two will first reach their specified values. For this we calculate a quantity called allowable bending moment denoted as M_all . This is the maximum bending moment that can be applied at the beam section. The steps for calculating M_all are as follows:

We can put f_c = σ_cbc in 2.23 to get M_all(c) with respect to concrete. Similarly, We can put f_st = σ_st in 2.24 to get M_all(s) with respect to steel. Thus:

Eq.2.28 and 2.29
M_all(c) =0.5b σ_cbc (kd)(jd)  and  M_all(s) =A_st σ_st (jd)

We must calculate both the above quantities and take the lesser value as M_all . The reason for taking the lesser value can be explained as follows:

Suppose M_all(c)  < M_all(s)   and suppose we take the higher value M_all(s) as the M_all . Then, when we apply this value of bending moment M_all(s) on the beam, eq 2.28 will not be satisfied (jd and kd  depend on the sectional properties and are independent of the moment applied). In such a situation, the stress in concrete will exceed σ_cbc making the beam unsafe.

Similarly, suppose M_all(s) < M_all(c)  and suppose we take the higher value M_all(c) as the M_all . When we apply this value of bending moment M_all(c) on the beam, eq 2.29 will not be satisfied. In such a situation, the stress in steel will exceed σ_st making the beam unsafe.

So we must always take the lesser of M_all(c) and M_all(s) as M_all 

Thus we calculate the appropriate value of M_all . We can calculate the load corresponding to this bending moment, so that the loading can be stopped before reaching it.  This marks the end of phase 2 and the beginning of phase 3.

We will take our discussion a little more further to see what happens after phase 2. We have seen that the phase 2 is also called 'Linear Elastic cracked phase', because the plot of stress in both concrete and steel can be represented by a straight line. That is., the stress will be proportional to strain. But when we move into the phase 3, the plot for concrete becomes a curve. This can be explained as follows: We know that at the end of phase 2, it is the top most layer in concrete, that has reached the limiting value of σ_cbc  . The layers below have a lesser stress value. So when phase 3 begins, it is the layers near the top that will be experiencing the next level of stress. At these higher levels of stresses, the stress is not proportional to the strain. This can be seen in a typical stress – strain curve of concrete. Fig 2.12 below shows such a curve.

Fig.2.12
Stress-Strain curve for concrete

The above curve is prepared from the readings obtained from the loading test on a concrete specimen in the lab. The curve has a straight line portion at lower strains. But when the strain increases, it becomes a curve. This ‘change into curve shape’ will be seen in the stress plot of a real beam cross section also. That is., the top region of the stress plot of the beam section becomes a curve. This is shown in fig 2.13 below:

Fig.2.13
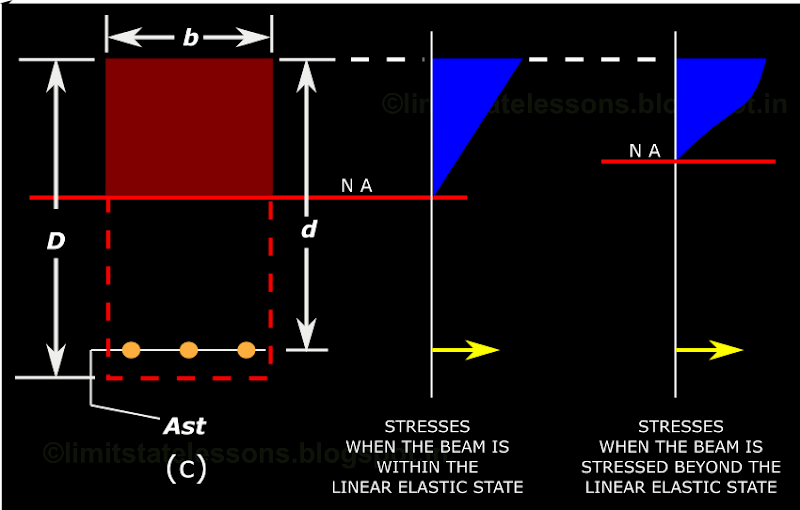
Stress takes a curved shape at the beginning of phase 3

In the fig above, the NA has shifted upwards when higher stresses are applied. The reason for this is explained in the discussions further down.

When the beam is loaded further, the lower layers also enter phase 3, and in the stress plot, the lower regions also becomes curve.

So we have seen that the phase 3 is a non linear phase. The behaviour of the beam in this phase depends on the amount of steel provided. Also we have to note the difference in behaviour of the steel and concrete: The reinforcing steel have a greater ductility. It can undergo greater strains than concrete. Yielding of steel occurs at higher stresses, and the amount of yield, which is measured as strain can be in the range 0.12 to 0.20, before failure of steel occur. But for concrete, this range is 0.003 to 0.0045. To get a better understanding of these ranges, we can think of two specimens, one of concrete and the other of steel. Let both of them have the same length of say 20 cm, then the maximum increase in length that the steel specimen can have is calculated as follows:

Strain =  Δl / l = 0.12 to 0.20. So Δl = 0.12 x 20 to 0.2 x 20cm = 2.4 to 4.0cm

Similarly, the decrease in length that the concrete specimen can have is calculated as follows:
Strain =  Δl / l = 0.003 to 0.0045. So Δl = 0.003 x 20 to 0.0045 x 20cm = 0.06 to 0.09cm

From the above, we can see that, when concrete and steel are combined to form a composite material, at higher stresses, the concrete will fail before failure of steel occurs.

The ability of steel to undergo large deformation can be seen from it’s stress strain curve:

Fig.2.14
Stress strain curve for steel

Steel has a flat, horizontal line portion after the yield point. This indicates that after yielding, steel can undergo greater elongation without any increase in stress. But concrete does not have such a portion.

It may be noted that the above stress strain curve for steel (fig.2.14) and that of concrete (fig.2.12), are drawn separately and in different scales. If we draw them together using the same scale, the difference will become more clear. Such a plot is shown below:

Fig.2.15

So at higher stresses, steel has begun to elongate, and when we gradually increase the load, steel elongates, but the stress in it remains constant. As the stress is constant, the Tensile force T in the steel is also remaining constant. The applied bending moment is resisted by the resisting moment of the beam given by Eq.2.22: M =T jd  But T is remaining constant.

So to resist an increasing load, the resisting moment can be increased only by increasing jd . This can be achieved only by shifting the NA upwards. It can be explained as follows: From fig.2.11, we can see that jd = d – kd/3. So to increase jd, kd must decrease. That is., the Neutral axis must shift upwards.

Due to this upward shifting of the NA, another effect will occur: The area of concrete available to resist compression will now be lesser. As the area of concrete decreases, the stress in it will increase and consequently the strain will also increase. As the concrete can sustain only very small strains, it will fail by crushing.

But before this failure of concrete occur, the steel has yielded to a greater extent. This cause the beam to deflect more and the cracks at the bottom side of the beam become wider. Such deflections and wider cracks give sufficient warning about the beam failure that is about to take place.

So the failure of the beam is by the crushing of concrete. But it was initiated by the yielding of steel under tension. This type of failure is called tension failure.

Now we will try to analyse the behaviour of a similar beam under the same loading conditions, but having a larger quantity of tensile steel. We increase the load on such a beam gradually from zero. Similar to the previous beam, the end of phase 1 is marked by M_cr  . The calculations for marking the end of phase 2 is also similar to the previous beam. We use Eq.2.25 and Eq.2.26 for marking the end of phase 2 for this beam also. If a large quantity of tensile steel is present, we can be sure that M_all(s) will be greater than M_all(c), and so the lesser quantity M_all(c) should be used to mark the end of phase 2.

The reason for M_all(s) being greater (when larger quantity of steel is present) than M_all(c) can be explained as follows: As we continue to increase the load after the end of phase 1, the steel will not yield because now it has a larger area, and is stronger. This situation can be viewed mathematically as follows: Tensile stress = Tensile force / Area of steel. As the area which is in the denominator has increased, the tensile stress has decreased. So the steel does not yield. In the previous beam, as the end of phase 2 approached, the steel yielded and entered the horizontal flat portion of the stress strain curve. So in it, the steel elongated under constant force. But here, steel has not reached the flat portion. So when the loading increases, the tensile force in steel also increases. To maintain the equilibrium, the compressive force C has to increase in such a way that C = T. The NA shifts downwards to increase the area of the region under compression, and thus to increase C. But eventually this increase in area becomes insufficient and the compressive stress and the strain in concrete begin to increase. The value σ_cbc  is reached in  concrete before σ_st  in steel is reached. So M_all(c) will mark the end of phase 2.

Now we increase the load on the same beam and enter phase 3. The stress in concrete has already reached it's permissible value, while steel is still safe. With the increase in load, the stress in concrete enters the non linear state and will fail by crushing. In the previous beam also, the failure was by crushing of concrete. But there is an important difference. In the present beam, the steel has not yielded. So there was no deflection for the beam and there were no wider cracks. So there was no warning about failure. This type of failure occurs suddenly and is called compression failure.

The present beam which has a larger area of steel is called an 'over reinforced beam'. While the previous beam which had a lesser area is called an 'under reinforced beam'. But we need a method to calculate how much is 'larger area of steel' and how much is 'lesser area of steel'. This is done by obtaining a quantity A_st,b  called the 'area of steel for a balanced section'.

Every beam section having a particular value of width b and effective depth d will have a particular value of A_st,b .

• If this section have an area of steel equal to A_st,b  then it is a balanced section.  
• If this section have an area of steel greater than A_st,b then it is an over reinforced section and
• If this section have an area of steel lesser than A_st,b  then it is called an under reinforced section.

Now we will discuss about a Balanced section in detail:In a balanced section, the tensile stress f_st in steel and the compressive stress f_c in concrete reach their allowable limits of σ_st and σ_cbc simultaneously. The analysis of a balanced section can be done based on the fig.2.16 below:

Fig.2.16
Stress distribution in a balanced section

The above section is provided with an area of steel equal to A_st,b , and is a balanced section. The notations for other quantities like neutral axis depth factor k, lever arm depth factor j, etc., have been changed from those in fig.2.11 above.  The notations are changed because these quantities are all constants for a section if the steel provided is equal to A_st,b . So they can be denoted by unique symbols. The changes are shown in the table 2-3 given below:

From the similar triangles in fig 2.16, Base of upper triangle = σ_cbc . Base of lower triangle = σ_st /m.
Altitude of upper triangle = k_bd . Altitude of lower triangle = d –k_bd.

So we get:

From this,

Eq.2.30

But from the discussion on modular ratio of reinforced concrete, mσ_cbc is a constant, whose value is given by the code as 280/3

So we can put mσ_cbc = 280/3 in Eq.2.30, and an equation for k_b can be derived as:

Eq.2.31

Thus we can see that the neutral axis depth factor k_b for a balanced section depends only on σ_st , the permissible tensile stress in steel. In other words, a particular grade of steel has a particular value of k_b. However for Fe 250, diameter of bar should be considered as specified in table 22 of the code. (Also see table 2.2 above)

A sample calculation of the value of k_b for Fe 415 steel can be done as shown below:σ_st  =230 for Fe415 steel.So k_b = 280 / (280 + 3 x230) = 0.2887

Now we can proceed to derive the other constants of a balanced section. From fig.2.15,

Eq.2.32

Calculation of p_t,b :
In Fig.2.16, the expressions for C and T has been derived in the same way as Eqs. 2.19 and 2.20 were derived.

Thus for a balanced section,

Eq.2.33 and Eq.2.34

C =0.5bk_bdσ_cbc and  T =A_st,bσ_st

Equating C and T we get

0.5bk_bdσ_cbc =A_st,bσ_st   Dividing both sides by bd we get

From this we get

Eq.2.35

 

Now we will derive the expression for M_bal :
We know that Moment = Force X Lever arm. So we have

Eq.2.36

M_bal = C j_bd

Substituting 2.32 and 2.33 in 2.36 we get

This can be rearranged as:


Eq.2.37

Thus we have computed the constants of a balanced section. Now we can learn a little more about under reinforced section.We have already seen it's properties.

For an under reinforced section:

• The area of steel A_st is less than A_st,b

• Tensile stress f_st in steel reaches the allowable limit of σ_st before the compressive stress f_c in concrete reach the allowable limit of σ_cbc   ie.,

Eq.2.38

f_st = σ_st AND  f_c < σ_cbc

• The allowable moment is limited by the permissible stress in steel σ_st , and not by the permissible stress in concrete σ_cbc .

With the help of the constants that we obtained for a balanced section, we can predict whether a section is 'under reinforced' or not.

We have seen earlier that the NA of an under reinforced section shifts upwards when the steel begins to yield. A mathematical procedure for proving this is as follows:

Fig.2.17 below shows the comparison between the stresses of a balanced section and an under reinforced section.

Fig.2.17
Comparison between stresses in a Balanced section and an Under reinforced section

In the above Fig.2.17 (a), the blue line is the plot of the stress in a balanced section. This blue line is shown again in (b) for comparison. Here the yellow line shows the plot for an under reinforced section. At the bottom point, σ_st /m remains the same. But at the top point, stress f_c  is less than σ_cbc . Thus the yellow line cuts the axis at a point above the NA of a balanced section. So for an under reinforced section,

2.39

kd < k_bd 

Now we look at the percentage of steel. We know that for an under reinforced section, A_st < A_st,b . So for an under reinforced section,

2.40

p_t < p_t,b

Where

which can be calculated from the properties of the given beam section, and p_t,b  can be calculated using 2.35.

So to determine whether a given section is under reinforced or not, either of the two conditions 2.39 or 2.40 may be checked.

If we determine that the given beam section is under reinforced, we can proceed to calculate the allowable moment M_all  . We have seen that the stress in steel will reach the allowable limit of σ_st first. So the allowable moment is given by M_all = M_all(s) = Force in steel x Lever arm = [Area of steel x stress in steel] x Lever arm

Thus for an under reinforced section,

 2.41

Now we must calculate the amount of compressive stress that the extreme fibre in concrete is subjected to, when this allowable moment is applied at the beam section. This can be done using two methods.

Method 1:Using the equilibrium condition C=T

First let us write the equations:

Eq.2.42 and Eq.2.43

C =0.5b kd f_c  and  T =A_stσ_st

In the above equations, the stress in steel is the limiting value of σ_st which is a known value given by the code, while the stress in concrete is denoted by f_c . This is because, in the under reinforced section, when the maximum allowable bending moment which is M_all = M_all(s) is applied, the stress in steel would have reached the allowable value of σ_st . While the stress in concrete would be somewhere below the maximum allowable value σ_cbc . So we cannot denote it by σ_cbc . Hence we use the symbol f_c , and our present aim is to is to derive an equation for finding the value of f_c .

Equating the two we get:

Eq.2.44

Method 2:From the similar triangles in fig 2.17(b),Base of upper triangle = f_c . Base of lower triangle = σ_st /m.
Altitude of upper triangle = kd . Altitude of lower triangle = d –kd.

From this we get

Eq.2.45

This completes the discussion about under reinforced sections in Working stress method. Now we can take up over reinforced sections.  We have already seen it's properties.

For an over reinforced section:

• The area of steel A_st is greater than A_st,b

• Compressive stress f_c in concrete reaches the allowable limit of σ_cbc before the tensile stress f_st in steel reach the allowable limit of σ_st ie.,

Eq.2.46

f_c = σ_cbc  AND  f_st < σ_st

• The allowable moment is limited by the permissible stress in concrete σ_cbc  , and not by the permissible stress in steel σ_st .

With the help of the constants that we obtained for a balanced section, we can predict whether a section is ‘Over reinforced' or not.

We have seen earlier that the NA of an over reinforced section shifts downwards when the load is increased. A mathematical procedure for proving this is as follows:
Fig.2.18 below shows the comparison between the stresses of a Balanced section and an Over reinforced section.

Fig.2.18
Comparison between stresses in a Balanced section and an Over reinforced section

In the above Fig.2.18 (a), the blue line is the plot of the stress in a balanced section. This blue line is shown again in (b) for comparison. Here the green line shows the plot for an over reinforced section. At the top point, σ_cbc  remains the same. But at the bottom point, stress f_st  is less than σ_st . Thus the green line cuts the axis at a point below the NA of a balanced section. So for an over reinforced section,

2.47

kd > k_bd 

Now we look at the percentage of steel. We know that for an over reinforced section, A_st > A_st,b . So for an over reinforced section,

2.48

p_t > p_t,b

Where

which can be calculated from the properties of the given beam section, andp_t,b  can be calculated using 2.35.

The above equations 2.47 and 2.48 are just the opposite of the equations 2.39 and 2.40 which we used in the case of an under reinforced section. So it is clear that the question as to whether a beam section is under reinforced or over reinforced, will be answered while using either of equations 2.39 and 2.40

If we determine that the given beam section is over reinforced, we can proceed to calculate the allowable moment M_all  . We have seen that the stress in concrete will reach the allowable limit of σ_cbc first. So the allowable moment is given by M_all = M_all(c) = Force in concrete x Lever arm = [Area of concrete x stress in concrete] x Lever arm

Thus for an Over reinforced section,

Eq.2.49

Now we must calculate the amount of compressive stress that the extreme fibre in concrete is subjected to, when this allowable moment is applied at the beam section. This can be done using two methods.

Method 1:Using the equilibrium condition C=T

First let us write the equations:

Eq.2.50 and Eq.2.51

C =0.5b kd σ_cbc  and  T =A_stf_st

In the above equations, the stress in concrete is the limiting value of σ_cbc  which is a known value given by the code, while the stress in concrete is denoted by f_st . This is because, in the over reinforced section, when the maximum allowable bending moment which is M_all = M_all(c) is applied, the stress in concrete would have reached the allowable value of σ_cbc . While the stress in steel would be somewhere below the maximum allowable value σ_st . So we cannot denote it by σ_st . Hence we use the symbol f_st , and our present aim is to derive an equation for finding the value of f_st .

Equating the two we get:

Eq.2.52

Method 2:From the similar triangles in fig 2.18(b),Base of upper triangle = σ_cbc  . Base of lower triangle = f_st /m.
Altitude of upper triangle = kd . Altitude of lower triangle = d –kd.

From this we get

Eq.2.53

Thus, when a singly reinforced beam section is given to us, we can determine whether it is Under reinforced or over reinforced. We can also determine the allowable bending moment, and the stresses in concrete and steel when this allowable bending moment is applied at the section.

This completes the discussion about the analysis of a singly reinforced rectangular section by working stress method. By taking the discussion further beyond the end of phase 2, we are able to learn about Tension failure, Compression failure, and also Balanced, Under reinforced and Over reinforced sections.

The following are the links to two solved examples which shows the application of the topics that we discussed above.

Solved example 2-2

Solved example 2-3

The discussion that we had above is about the ‘analysis’ of beam sections by working stress method. This discussion will give a basic idea about the behaviour of beams under flexure, and will form a foundation for the better under standing of the Limit state method.

The ‘design’ using working stress method method is not discussed here. But it is worth mentioning that while designing a section, it should be designed as an ‘Under reinforced section’. This is because, if an under reinforced beam is overloaded to failure, the failure will not be a sudden one. There will be warning signs in the form of deflections, wider cracks etc.,

Finally, we will have a quick look at the ‘method of application of loads in working stress method’. We will do this by using an example. Let us assume that using Working stress method, we want to design a beam to carry a sign board. Let us also assume that the beam has to carry the sign board only. That is., there are no other loads coming on the beam except the self weight of the beam and it’s finishes. We begin the design by calculating the wt. of the sign board. This can be done by finding the wt. of the individual components separately and then adding up. For example, if the board consists of 45 x 6mm steel flats, then, from data book, the mass of this flat per meter length = 2.1 kg/m. If there is a total length of 5m of this flat in the board, then the total mass = 2.1 x 5 = 10.5 kg. This mass should be converted to weight by multiplying with 10. So the total weight of flats = 10.5 x 10 = 105 N = .105kN. In this way the total wt. of all the components of the sign board can be calculated from the values given in the data book.

In the working stress method, this total wt. of the board can be directly used in the design. That is., the bending moment is calculated for this wt., and that BM is used in the design. Thus we are using the ‘working’ loads. These loads are also called ‘characteristic loads’. So what about the safety factor? The factor of safety is introduced by limiting the permissible values of stresses in materials: concrete and steel. (Tables 2-1 and 2-2). Safety factors are not applied to loads.

But in the Limit state method, the safety factors are applied to both loads and materials. As we saw in chapter 1, the Partial safety factor for DL = 1.5. And the stresses in materials concrete and steel should be obtained only from the design curves in Figs.21 and 23 of the code.

It may be noted that the above example of a sign board is used for a basic demonstration of the ‘method of application of loads in working stress method’ only. The actual design will involve a lot more calculations. Some of them are:

• LL during erection and maintenance. 
• Wind loads and seismic loads.
• The nature of load (whether concentrated loads or continuous loads).
• Stability and strength of the supports of the beam.
• Proper anchorage of beam into these supports.
• Proper anchorage of the board into the beam.

In fact, all the relevant clauses of the various codes that are applicable, should be satisfied.   

In the next section, we will discuss the analysis by the Limit state method.

PREVIOUS

NEXT

              Copyright©2014 limitstatelessons.blogspot.com- All Rights Reserved