In the previous section we completed the discussion on 'load calculation on a transverse stair'. Link to a solved example which illustrates the analysis and design is given below:
Solved example 16.3
The reinforcement details according to the above solved example is shown in the figs.16.64 and 16.65 given below:
Fig.16.64
Sectional elevation of transverse stair
Fig.16.65
Section XX
We will now discuss the various features of the above two figs:
The main bars are given as the bottom most layer. The distributor bars are given as the second layer from the bottom. This arrangement will give maximum possible effective depth ‘d’ for the section. From the section XX, we can see that the main bars are given two 90o bends at both the ends. This will give a 'hook' like arrangement at both ends. The top portion of these 'hooks' will act as the steel required for resisting any possible hogging moment at the supports. The length required for this top steel is 0.15l, where l is the effective span of the waist slab. But the area required for this top steel is only half of that at the mid span. So, as shown in the inset, only alternate bars are given these hooks.
The distributor bars are of mild steel. So the symbol Φ is given to denote them.
In the above example, only a part plan (shown in the fig. below) of the stair was given along with the problem data.
Problem data of solved example 16.3:
This is because, this small portion is sufficient for defining the problem of this type of a transverse stair. But some times, this stair may have a landing also as shown below.
Fig.16.66
Landing in a transverse stair
In this case also the sloping portion can be analysed and designed by the same procedure, and the landing can be analysed and designed as a simply supported one-way slab.
Stairs cantilevering from the side of a beam
The following fig.16.67 shows the part view of a stair.
Fig.16.67
View of a cantilever stair
It is projecting from the side of a wall. The wall is shown in a finished state. So we cannot see more details. The fig. below shows the view before the plastering is applied to the wall.
Fig.16.68
View of a stair cantilevering from a stringer beam
We can see that the stair is projecting from the side of a beam, which is concealed inside the wall. In actual construction, the beam (which frames into columns) and the waist slab will be casted first, and after curing and removal of form works, the masonry wall will be constructed above and below the beam. The elevation and section are shown in the figs. below:
Fig.16.69
Part elevation view of cantilever stairs
Fig.16.70
Section XX
The waist slab bends in a direction perpendicular to the direction of travel of the pedestrians, and so it is a transverse stair. The load calculation procedure is the same as that for the transverse stair supported on two stringer beams. So we can use the same Eq.16.25 for the loads. The line diagram for the analysis will be as shown below:
Fig.16.80
Line diagram for cantilever stairs
The effective span l of the cantilever (cl.22.2.c) is the length of the cantilever up to the face of the support plus half the effective depth. For initial proportioning, we can assume the thickness of waist slab to be clear length of cantilever/10 . However, this should be finalized only after the complete design and doing the various checks.
In the next section, we will see a solved example of the above type of stairs.
In the previous section we saw the self weight of the waist slab and steps. In this section we will see the other loads.
3) Wt. of finishes: As in the case of longitudinal stairs, we obtain this from codes or data books. Let us denote this load as wf,data. We know that this is specified on 1m2 horizontal area. But we are having an inclined area. If we take the exact value from the code or data book, we will be using an excess quantity of load as shown below:
Fig.16.57
Horizontal 1m exceeds inclined 1m
[We are using the symbol ‘wf,data’ for denoting the wt. of finishes that we obtain from codes or data books. In the case of longitudinal stairs, we did not use such a symbol for the wt. of finishes. The reason is that, for longitudinal stairs, the 'values from codes or data books' is applied directly in the calculations. But here in the case of transverse stairs, as we will soon see, a modification have to be applied to it. So it is convenient to denote it using a symbol.]
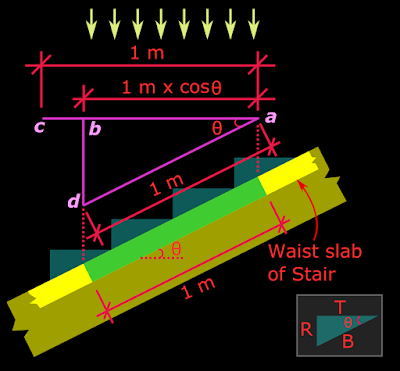
From the fig.16.57 we can see that the length ac which is equal to 1m is greater than the horizontal projection of the green coloured area. So we need to take a lesser length on the horizontal plane. This lesser length can be determined using the following fig.16.58
Fig.16.58
Lesser length on the horizontal plane, which corresponds to the 1m on the inclined plane
From the two red dotted lines we can see that ab is our required 'reduced length'. This can be calculated from triangle abd, [Note that ad = 1m. This is because ad, the two red dotted lines, and the green strip, are the sides of a Parallelogram] We get ab = 1m x cosθ. Here θ is the angle at a. So our next step is to calculate θ.
By using the 'theorem of alternate interior angles', θ is also the angle that the waist slab makes with the horizontal. By using the same theorem, it is also the angle at the upper corner of a step, as shown in the inset of the above fig.16.58. So we will get the value of θ from the relation: cosθ = T/B, where ‘B’ is the hypotenuse of a step, given by B = √(R2 + T2) .
So we can easily calculate cosθ. Now, 1 x Cosθ = cosθ = the required reduced length. The length perpendicular to the plane of the paper is 1m. So the reduced area = cosθ x 1m = cosθ m2
So we determined the 'reduced area' that is to be used. Now, wf,data is the load in 1m2. So the load in the new reduced area = wf,data x cosθ. So we can write:
Eq.16.22: The load from finishes on 1m2 area on the inclined surface = wf,data x cosθ
4) Live load: This is also specified in the codes and data books as load per 1m2 on horizontal area. So following the above discussion, we will denote it as wLL,data , and write:
Eq.16.23: The load from LL on 1m2 area on the inclined surface = wLL,data x cosθ.
Thus we get all the four items that constitute the load on the waist slab. We add these four, and denote the sum as W. Thus:
Eq.16.24: W= Sum of the four quantities calculated using Eq.16.20, 21, 22 and 23
Now we need to understand the effects of this load on the stair. Let us analyse:
The W acts vertically as shown below:
Fig.16.59
Total load W acting vertically downwards
This W can be resolved into two components as shown below:
Fig.16.60
Components of the vertical force W
One component acts perpendicular to the slab and the other acts parallel to the slab. From the triangle shown in the inset, we can see that the angle between W and the component perpendicular to the waist slab is equal to θ. So the magnitude of this perpendicular component will be equal to W cosθ. And the magnitude of the component which is tangential to the sloping surface of the waist slab will be equal to W sinθ.
Now we will see the effect of these two components. We will see the effects separately. The effect of the perpendicular component is shown in the view given below:
Fig.16.61
Effect of perpendicular component
From the above view, we can see that the perpendicular component will bend the plane surface of the waist slab into a three dimensional surface. That is., the plane surface bends to become the surface of a cylinder. The effect of the tangential component is shown in the view below:
Fig.16.62
Effect of Tangential component
We can see that tangential component does not bend the slab into any three dimensional surface. Instead, it causes the slab to bend in it's own plane. Here we must understand the difference between these two types of bending.
• In the first case, when the slab is bent into a cylindrical shape, only the thickness 't' of the slab is available to resist the bending.
• But in the second case, when the slab bends in it's own plane, a very large depth is available to resist the bending. For example, if we are considering a 1m wide strip, the whole 1m will be available to resist this bending.
So the tangential component is ignored in the design. We provide steel to resist the perpendicular component only.
We have discussed earlier about the design of simple horizontal slabs.
• In simple horizontal slabs, the slab member is horizontal, and the loads acting on them are vertical. So the loads are acting perpendicular to the slab surface.
• In the transverse stairs, when the tangential component is ignored, they become an inclined slab acted upon by loads perpendicular to it's surface.
Both are same: A slab surface acted upon by forces perpendicular to it. So we can design transverse stairs in the same way as a simple horizontal slab.
Thus we reach a conclusion: We calculate W and multiply it with cosθ. The product 'Wcosθ' is the load which will act perpendicular to the slab surface. We provide reinforcements to resist this Wcosθ.
This Wcosθ is the load acting on 1 m2 area on the inclined surface. We are designing the slab as a 1m wide strip. So this is the same load on 1m length of the strip. (See the explanation based on fig.5.11.) So we can write:
Eq.16.25
The UDL per meter length on 1m wide strip of a transverse stair = w1 = Wcosθ.
• where W= Sum of the four quantities calculated using Eq.16.20,21,22 and 23
• and cosθ = T/B
When the above calculations are done, we can draw the line diagram of the 1m wide strip as shown below:
Fig.16.63
Line diagram for a 1m wide strip of a Transverse stair
In the above line diagram, the slab is shown to be simply supported. So the maximum bending moment at midspan can be obtained as w1l2/8. If the ends are fixed, or if the slab is continuous over a number of supports, detailed analysis should be done.
To begin the analysis and design, we must know the self weight of the waist slab. For calculating the self wt., we must know the cross sectional dimensions. The width is fixed at 1000 mm, as we are considering a 1m wide strip. We want the depth.
For a preliminary design, we can use a thump rule: Upto a clear span of 2m, a value of 100mm can be assumed for ‘t’ of a transverse stair supported on two stringer beams or walls. However, this value should be finalised only after doing the various checks like check for deflection, shear check etc.,
In the next section we will see a solved example based on the above discussion.
In the previous section we saw an example which gives the basic details about transverse stairs. In this section we will discuss more details. The fig.16.51 below shows the sectional elevation of the stair in the example that we saw.
Fig.16.51
Sectional elevation of stair
In the above figs., the waist slab is resting on the top of the stringer beams. Another arrangement possible is that in which the beams are projecting above the stair. The view and sectional elevation of this arrangement are shown in the figs.16.52 and 16.53, below:
Fig.16.52
View of stairs with projecting stringer beams.
Fig.16.53
Sectional elevation of stairs with projecting stringer beams
In the above fig. we cannot expect flange action because the flange will be in tension. So we must design it as rectangular beams.
Yet another arrangement that is possible, is to use masonry walls instead of beams. This can be used if adequate foundation can be provided for the walls, and also if the height of walls can be kept within permissible limits.
In all the above methods, the waist slab will be spanning in a direction, perpendicular to the direction of travel, and so it is a transverse stair.
Loads on a Transverse Stair
Let us now analyse the loads acting on this transverse stair.
In the case of a longitudinal stair, we determined the load on a horizontal projection having an area of 1 m2, as shown earlier in fig.16.16. But for a transverse stair, we use the loads on a 1 m2 area, on the inclined slab itself. This is shown in the fig.16.54 below:
Fig.16.54
1 m2 area on inclined surface
The method of using such a load is used for the 'analysis and design of the stair' will be explained later. At present let us determine the magnitude of this load. It has four items as given below:
1) Self wt. of waist slab: This can be calculated based on the sectional view in fig.16.55 given below:
Fig.16.55
Self wt. of waist slab
• The area of the portion coloured in green in the above fig. is 1 x t m2. (‘t’ is in m). Note that the '1m' here is the same 1m marked perpendicular to the red strip in the previous fig.16.54
• The length of the block (perpendicular to the plane of the paper) is 1m. This '1m' is the same 1m marked parallel to the red strip in the fig.16.54
So volume = 1 x t x 1 = t m3.
Thus the wt. of this block having an area of 1m2 = t x 25 = 25t kN. where 25 is the unit wt of concrete in kN/m3.
Thus we can write:
Eq.16.20: Self wt. of waist slab = 25t kN/m2
2) Self wt. of steps:
• Area of cross section of 1 step = [0.5 x R(Rise) x T(Tread)] (∵area of the triangle = 0.5 x Base x Altitude)
• Length of the triangular prism perpendicular to the plane of the paper = 1m. This '1m' is the same 1m marked parallel to the red strip in the fig.16.54
• So volume = 0.5 x R x T x 1 =0.5RT
• Thus wt. of one step with a length of 1m perpendicular to the plane of the paper = 0.5RTγs Where γs is the unit wt. of the material of the step. (For brick masonry, γs = 20 kN/m3)
Now we have to calculate the no. of such steps with in the length of 1m shown in fig.16.55. For that, we will use the fig.16.56 given below:
Fig.16.56
No. of steps in 1m along the slope
From the fig., it can be easily seen that the no. of steps within the two red dotted lines will be equal to 1m divided by 'B' where B = √(R2 + T2) (∵ B is the hypotenuse of the triangle with base T and altitude R)
So we can write
Eq.16.21
The total wt. of all the steps within the 1m2 area =
It may be noted that 1/B will be a 'whole number + a fraction' in most cases. The fractional part indicates that 'parts of steps' will also be coming in the 1m2 area.
The next item is the ‘weight of finishes’. We will see the details about it in the next section.
In the previous section we saw the arrangement of the stair in plan and sectional elevation views. We calculated the loads also. It appears as an ordinary longitudinal stair. In this section we will see how the load distribution is modified when the flight is given an embedment into the side wall. Later in this section, we will begin our discussion about 'transverse stairs'.
From the figs. in the previous section, we can see that the load on the Going is transferred to the ground at the bottom end and to the beams at the top end. But if the waist slab of the Going have some embedment into the side wall of the main building, then some load will be transferred to that wall also. Cl.33.2 of the code gives us the details about the load distribution when such an embedment is provided. For this clause to be applicable, the embedment that is provided, should not be less than 11 cm. Consider the modified plan of the stair given below:
Fig.16.47
Modified plan
The waist slab has an embedment of 12 cm into the wall of the main building. As this is greater than 11cm, we can apply the clause to the stair. The section xx is given in fig.16.48 below. This sectional view helps to calculate the loads based on the clause.
Fig.16.48
Section XX
We know that the load is acting on the whole width 'W' cm of the stair (W =90cm for our stair). But when a minimum embedment of 11cm is provided, the load is assumed to act on a reduced width of (W – 15cm). This is shown in the fig.16.48 above.
Let us see how we can apply this to our stair:
We have calculated a load of 20.16 kN/m2 on the Going. If there is no embedment, the total load on the whole area of the Going will be equal to 20.16 multiplied by the total area of the Going. This is equal to 20.16 x 0.9 x 4.0 = 72.576 kN. (here 4.0 is the effective span of the Going)
As there is an embedment of 12 cm in our case, the total load can be modified as 20.16 x (0.9 – 0.15) x 4.0 = 60.48 kN. [Where (0.9 – 0.15) is the reduced width]. So we can discard 72.576 and use 60.48 kN.
Now, one more modification have to be made:
When a normal longitudinal stair bends, the width that resists the bending is W. But when the embedment mentioned above is available, the effective width of the stair, that resists the bending can be assumed to have an increased value. According to the code, this increased value is (W + 0.075). This is also shown in the fig.16.48 above.
So the load is acting on an area of [(W +0.075) x effective span ]. Thus, dividing the total load by this new area will give us the new load per 1 x 1 m square area. In our case, this is equal to 60.48 / [(0.9 + 0.075) x 4.0] = 15.51 kN/m2. So for the analysis and design, we can use a UDL of 15.51 kN/m instead of 20.16 kN/m.
The difference is transferred to the side wall. In our case, the wall is resting on the ground. So there is foundation to take up this extra load coming on the wall. But if the wall is resting on a beam, then that beam will have to be designed for an additional UDL per meter length. In our case, this additional load = 20.16 - 15.51 = 4.65 kN/m. [The landing portion of our stair does not have any such embedment. So no modification needs to be applied to the load on the landing].
It should also be noted that, this method of giving an embedment in the side wall for a longitudinal stair causes construction difficulties, and so, it is not generally used in practice.
Transverse Stairs
We have already seen a schematic diagram of a transverse stair here. Now we will discuss the detailed analysis and design procedure. The fig.16.49 below shows the view of an office building. It has a Basement floor, Ground floor and a First floor. The floor level of the Ground floor is at some height above the surrounding Ground surface. So a stair is provided for the access to the ground floor. Also there is open space between the basement of the building and the surrounding earth. So the stair acts as a 'bridge' also.
Fig.16.49
Example of a Transverse stair
The next fig.16.50 below shows the details of the stair. A portion of the earth filling below the Ground level is removed to get a clear picture. A portion of the stair is also removed to see the waist slab.
Fig.16.50
Detailed view of Transverse stair
We can see that the brick work of the steps is resting on the waist slab. The waist slab is resting on two beams on the sides of the stair. These beams are called stringer beams. Each of the stringer beams are resting on columns:
• Column in the retaining wall support the lower end of the stringer beam
• Column in the main building support the upper end of the stringer beam
• The waist slab spans between the two stringer beams.
So the waist slab spans in a direction, which is perpendicular to the direction of travel of the pedestrians. In other words, the span is in the direction of the transverse axis of the stair. So this is a transverse stair.
The slab is simply supported on the two beams, and the span can be taken as the center to center distance between the two beams. [Though it is assumed to be simply supported, some top steel should be provided at supports to resist any hogging moments that may develop]. We have already discussed the design of beams earlier. So, in our present discussion, we are concerned with the analysis and design of the waist slab only.
It may be noted that, in the above views, finishing works are not yet applied on the stairs, while the main building is shown in a finished condition. So the brick works for the steps have to be done in such a way that, when the tile is laid on the top most step, it's top surface will be in the same level as the top surface of the tile of the floor of the main building. In the next section, we will see more details about this stair.
In the previous section we completed the analysis and design of a stair in which flights are supported on the landings. In this section we will discuss about a different kind of 'load distribution', that occurs in special type of longitudinal stair. Fig.16.43 below shows the external view of a building.
Fig.16.43
External stair of a building
A room is constructed as an 'extension' to the Main building. The stair climbs upto the roof of this extension room. This roof is at a lower level than the roof of the main building. From the top of this lower roof, another smaller stair is provided, which can be used to climb up to the roof of the main building. This smaller stair is built at the rear of the building, separately from the main stair, and is not seen in the view. We are concerned about the main stair in our present discussion. The section and plan of the stair are shown below:
Fig.16.44
Section of stair
Fig.16.45
Plan of Stair
We can see that the stair is supported on the ground at the bottom end, and on a beam at the top end. This is a longitudinal stair. The lower roof acts as the landing. The loads on the Going and the Landing are calculated below:
Four items constitute the load on the Going, and is given by Eq.16.9.These four items are:
1) Self wt. of waist slab on a horizontal 1m2 area (in kN/m2) =
= 5.991 kN/m2 .
2) Self wt of steps per 1m2 of horizontal area (in kN/m2) = (R γs) ⁄2 = 0.5Rγs
The value of γs for brick masonry is 20kN/m3
= 1.65 kN/m2
3) Self wt. of finishes per 1m2 of horizontal area (in kN/m2)
= 0.8 kN/m2 (obtained from code)
4) Live Load per 1m2 of horizontal area (in kN/m2)
= 5 kN/m2 (obtained from loading code)
Sum of above four = 13.441 kN/m2
So factored load = w1 = 13.441 x 1.5 = 20.16 kN/m2
Similarly, Three items constitute the load on the Landing, and is given by Eq.16.10. These three items are:
1) Self wt of steps per 1m2 of horizontal area (in kN/m2) = 25t (where ‘t’ is the thickness of the landing)
= 25 x 0.12 = 3.0 kN/m2
2) Self wt. of finishes per 1m2 of horizontal area (in kN/m2)
= 0.8 kN/m2 (same as for Going)
3) Live Load per 1m2 of horizontal area (in kN/m2)
= 5 kN/m2 (same as for Going)
Sum of above three = 8.8 kN/m2
So factored load = w2 = 8.8 x 1.5 = 13.2 kN/m2
Half of this load (0.5 x 13.2 = 6.6 kN/m2) can be assigned in the design of stairs because the full load will be used for the design of the landing slab. The line diagram of the stair is shown in the fig.16.46 below. Note that it is a continuous structure. This because of the intermediate support at B.
Fig.16.46
Line diagram for the stair
It can be seen that the above line diagram is incomplete. The length l2 is missing. We can easily obtain l2 from the architectural drawings. Once l2 is known, we can analyse the stair as a strip of a continuous slab, and the design can be done. But as mentioned earlier, the aim of our present discussion is to learn the details about a special kind of load distribution in longitudinal stairs. We are not doing the analysis and design of this stair. We are not concerned about the portion BC in our present discussion. In fact, we are going to focus our attention only on the portion from A to B, the ‘Going’ portion. We will discuss about it in the next section.
In the previous section we saw the loads on the flight of a stair which is supported on landings. In this section we will see the loads on the landings.
Part 2: Loads on the Landings:
In part 1, we have calculated w2. We have seen that it is calculated by the same method that we would use for calculating the w2 of an ordinary longitudinal stair. (See Eq.16.10). This is the original load on the landing. It is obtained on a 1 x 1 m square area.
There is more. w2 calculated above is the original load on the landing. But the landing is supporting the flight also. So the load from the 'Going' will also come on to the landing. Let us see how this load from the Going is distributed on the landing.
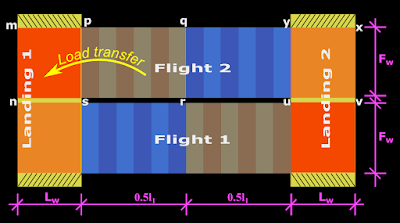
We have the load w1 on the Going. It is the load per 1 x 1 m sq. area (horizontal projection). So, once we calculate w1, we will be able to calculate the total load on the going. From the fig.16.41 below, this will be equal to w1 x Fw x l1.
Fig.16.41
Transfer of loads from the Going to the Landing
Where Fw is the width of the flight and l1 is the clear length of the Going. This is the total load acting in the total length of the Going. Half of this will be transferred to one landing and the other half to the other landing. So in the fig.16.41, the load from pqrs will be transferred to the landing 1. Similarly the load from qruy will be transferred to the landing 2.
So now we know the magnitude of the load which is transferred from the Going to the landing. Next we must know how this much load is distributed on the landing. This is also shown in the fig 16.41. The load from pqrs is assumed to be distributed uniformly on the corresponding area pmns of the landing. As the load is uniformly distributed, we can divide the load by the area to get the load per 1 x 1 m sq.
• Load on pqrs = 0.5w1Fw l1
• Area of mnsp = Fw Lw .(Where Lw is the width of the landing).
So load per unit area =
This is the load on one half (mnsp) of the landing. The other half will also be subjected to the same load because it is supporting the other flight. Thus the whole landing is carrying the load 0.5w1l1 / Lw.
So we have obtained the two loads:
• The original load on the landing = [w2] per sq.mt
• The load coming from the Going = [0.5w1l1 / Lw] per sq.mt
The sum of the two will be the total load acting on the landing per sq.mt. Thus:
Eq.16.19: The total load acting on the landing per sq.mt =
What role does this 'total load' play in the analysis and design of the landing slab? Let us find out:
The landing slab is designed as a One-way slab. It spans between the hatched portions shown in fig.16.41. We have already seen the design of one-way slabs here. We have seen that the load on a 1 x 1m square area of the slab is the same UDL per meter length, that is required for the design of a 1 m wide strip. So we conclude that, the above 'total load' is the UDL per meter length that we require to design a 1m wide strip of our landing slab.
So we have the methods to obtain all the loads on the stair. With these loads, we can do the analysis to find the Bending moments and shear forces. Once they are calculated, we can do the design.
We will now do the analysis and design of our stair. It is given as:
Solved example 16.2
The arrangement of bars according to the design in the above solved example is shown in the figs.16.42 given below:
Fig.16.42
Reinforcement details of Going and Landing
Now we will discuss some details about the above fig.
As in previous examples, bar ‘a’ becomes top bar in the top landing, and to compensate for this, bar ‘b’ is provided at the same diameter and spacing as ‘a’. Also, ‘a’ and ‘b’ are given enough embedment as explained earlier on the basis of fig.16.25. At the bottom intermediate landing, ‘c’ and ‘d’ are provided to resist any possible hogging moment. When there is hogging moment, these bars will be in tension, and so in order to prevent them from straightening up, they are given enough embedment in accordance with fig.16.25.
One more type of bar, named as ‘e’ is provided at the top landing. The reason for providing these bars can be explained as follows: The stair is supported on the landings. The support for the flight comes from the interior portion of the Landing. But the inner edge of the Landing (the line of intersection between horizontal landing portion and inclined flight portion) is also capable of providing some support. So the edge will act as an intermediate support of a continuous system. We know that hogging moments will develop at intermediate supports, and so top steel will have to be provided. Thus ‘e’ is provided to resist this hogging moment.
Another point that we have to note is the position of the main bars of the Landings. We can see that it is provided as the bottom most layer. This will give maximum effective depth, and so the ‘Moment of resistance’ MuR of the section of the Landing will be more. But in any case , these bars should indeed be the bottom most layer because, they have to provide support to the stair by carrying the bars(‘a’, ‘b’, ‘c’, ‘d’ and ‘e’) of the stairs. And in order to carry them, the bars of the Landing should be the bottom most layer.
Distributor bars for the Landing need not be designed because the bars of the stairs are coming in a transverse direction to the main bars of the Landing.
A small amount of steel (#8 @ 200 c/c) is also provided as top bars for the Landings. These bars will resist any hogging moment developed at the supports (the hatched portions in fig.16.41 above) of the Landings, and will also assist in tying the top bars of stairs, and thus to keep them in position.
It may also be noted that in the above fig., bars of different types are shown separately only for clarity. This was explained earlier based on the fig.16.25(b).
In the next section, we will discuss the load distribution in a particular type of longitudinal stairs.
Towards the end of the previous section we saw that the supports provided to the flights of the stair is unclear from the plan and sectional views. To get a clear picture of how the flights are supported, we will now see some 3D views of the building. The direction of views can be understood from the 'North direction' which is indicated in the key plan given in the previous section.
Fig.16.36
View from South East
Fig.16.37
View from North East
Fig.16.38
View from North West
We can see that, two brick walls are built, one on Bm1 and the other on Bm5. The brick wall over Bm5 can be seen in the sectional view that we saw earlier in fig.16.35. These two walls are parallel. The intermediate landing is supported by these two walls. That is., the intermediate landing is a one-way slab, spanning between these two walls. So at B, the flight AB can rest on this landing. In the same way, at C, the flight CD can also rest on this landing. Thus there is no need to take the flights up to Bm 3 at the rear of the building.
What about the supports at A and D? We can see that at A, there is a landing (at Floor1 level) in between Bm1 and Bm5. This landing is designed as a one-way slab spanning between these two beams. Then, the flight AB is supported on this landing at A.
There is an exact duplicate of this landing, directly above it (at Floor2 level). It spans between Bm1 and Bm5. Flight CD is supported at D on this landing. Thus there is no need to take the flights up to Bm 4 in the front of the building.
So we can summarize the support details as follows:
Flight AB is supported between two landings. One landing at A and another landing at B
The landing at A is at level 1. It is a one way slab spanning between Bm1 and Bm5
The landing at B is the intermediate landing of the stair. It is a one way slab spanning between walls built over Bm1 and Bm5
Flight CD is supported between two landings. One landing at C and another landing at D
The landing at C is the same intermediate landing on which end B of the first flight AB is supported
The landing at D is at level 2 It is a one way slab spanning between Bm1 and Bm5. This landing is an exact duplicate of the landing at A of the first flight.
It must be noted that in this type of stairs, special care should be taken while fixing up the arrangement and position of bars of both the sloping portions and the landings. We will see the details about it when we design the reinforcements of this type of stairs.
From the above discussion, it is clear how flights are supported on landings. The whole width of the landing slabs (1.2m in our case) is taking part in supporting the flights. But when we calculate the effective span of the flight, we can consider only a certain portion of the width. To determine this width, we will use the diagram shown below:
Fig.16.39
Portions of landings that can be considered for calculating Effective span
The width of the first landing is 2X and that of the second landing is 2Y. (Here X and Y are in m). Such a notation using 'twice X and Y' is only for the ease of presenting the formula. The widths need not be exact multiples of 2. It only implies that, whatever be the widths of the landings, half of those widths should be used for the calculations. (The hatched portions shows the support available for the landing slabs. These portions are not of any significance in our present discussion about effective span). The steps involved in the calculations are as shown below:
Step 1:
Determine X, half the width of the first landing.
Then, a certain length (denoted as 'Quantity 1') is determined as follows:
IF X is less than 1 m, THEN, Quantity 1 = X
IF X is greater than 1 m, THEN, Quantity 1 = 1 m
This simply means that Quantity 1 = the lesser of {X ; 1 m}. It can be presented in a graphical form as shown below:
Step 2:
Determine G, the Going.
Let Quantity 2 = G
Step 3:
Determine Y, half the width of the second landing.
Then, a certain length (denoted as 'Quantity 3') is determined as follows:
IF Y is less than 1 m, THEN, Quantity 3 = Y
IF Y is greater than 1 m, THEN, Quantity 3 = 1 m
This simply means that Quantity 3 = the lesser of {Y ; 1m}
Step 4:
This is the final step in which we just add the above three lengths. The sum thus obtained is the effective span. Thus:
Eq.16.17
Effective span = Quantity 1 + Quantity 2 + Quantity 3
From the method of calculation of Quantity 1 and Quantity 3, we can say that,
only half the width of a landing can become part of the effective span.
Also, if this half width is greater than 1m, then, only 1m can become part of the effective span.
If we analyse the above calculations, we can obtain one more inference:
Eq.16.18
If width of each of the two landings is less than 2m, then, we can calculate the effective span directly as:
Effective span = c/c distance between the landings.
So we can add these details to the above fig.16.39, and modify it as shown below:Fig.16.40
Effective span of flights supported on Landing slabs
Load calculations
The design of this type of stair has two parts.
In the first part, we design the flight which has an effective span obtained using 16.17.
But this flight has to be provided with adequate support on the landing slabs. So the design of landings is done as the second part.
So we will do the calculations of the loads also in two parts. In part 1, we will calculate the loads on the flight, and in part 2, we will calculate the loads on the landing.
Part 1: Loads on the flight.
From the fig.16.40 above, we can see that when we determine the effective span of the flight, we are getting a line diagram with two landings of lengths l2 and l3 , and a Going with length l1 . This is same as the line diagram (fig.16.21) of an ordinary longitudinal stair supported on walls or beams, that we saw at the beginning of the chapter.
So the methods for load calculations are also the same:
• The sloping portion has 4 load components which make up w1 (Eq.16.9),
• and the landing portions have 3 load components which make up w2 (Eq.16.10).
Thus we can easily compute w1 on the sloping portion and w2 on the landing portions. [It may be noted that even if the flight is not symmetrical (the widths of landings not being equal), w2 will be the same on both the landings, as w2 is the load per unit area. But for this, both the landings should have the same thickness.]
After computing w1 and w2, a modification has to be applied to w2. Recall that a modification to w2 was made in the case of 'stairs at right angles' which we saw in the previous section. Here also the modification is required because, w2 is resisted by both landing and the flight. But there is an important difference. It can be explained on the basis of the following fig:
Fig(a) shows the landing of a right angled stair and Fig(b) shows the flights supported on landings. Consider the upper flight in (b).
• The load w2 on the landing will contribute towards the bending of this flight.
• The load w2 will cause the bending of the landing also.
• So some portion of w2 is resisted by the flight and the remaining portion is resisted by the landing.
• But the portion resisted by the flight will 'come back on the landing' because, the landing itself is a support for the flight.
• This is different from the situation in fig(a), in which the flight is not supported on the landing, but on a separate wall or beam.
■ As the 'portion of w2 resisted by the flight', comes back to the landing, no reduction should be applied to w2 while analysing the landing.
■ A reduction of 0.5 can be applied to w2 while analysing the flight because, the flight will not be resisting a full w2.
With this modification applied, part 1, the load calculation on flight is complete. When those loads are calculated, we can find the moments and reactions. If the flight is symmetrical, we can use the same equations Eq.16.15 and 16.16 (which we derived for simple longitudinal stairs) to find the reactions and the moments. In the next section, we will see part 2, the load calculation on landing.