In the previous section, we completed the discussion on design of a doubly reinforced beam section. In this section we will discuss the analysis. When we are given a doubly reinforced beam section for analysis, we have to find the depth of the neutral axis xu , and the ultimate moment of resistance MuR.
We know that when we analyse the section using the Limit State Method, we are calculating the forces in the section at the point of impending failure. The concrete at the extreme compression fibre will be about to crush. And also, if it is an under reinforced section, the steel in the tension zone would have yielded.
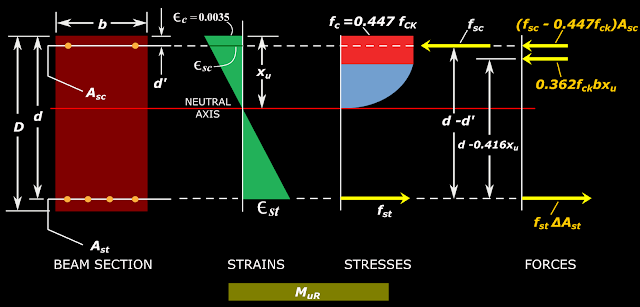
So now we are going to find the forces in a doubly reinforced section, at the above mentioned point of impending failure. We can base our discussions on the fig.12.1 given below:
Fig.12.1
Stresses, strains and forces
The above fig. shows all the stresses and forces at the ultimate state. We will now see the details of each component:
The depth of NA is denoted as xu. It's value can be less than or greater than xu,max, depending on the quantities of steel. It is one of our aims to calculate this xu of the given beam section.
We have derived the expression for εsc in the previous chapter. We used the triangles above the NA in the strain diagram. We have the same strain diagram here also. The only difference is that xu,max is now changed to xu. So from Eq.11.1, we get:
Eq.12.1:
When we know εsc, we can calculate the stress fsc in Asc. But here we cannot use the table 11.1 because, the values in it correspond to the condition of xu = xu,max. Here we are having xu, which may be having a value higher or lower than xu,max. So we have to use the original tables for calculating fsc.
The net compressive force in steel is obtained as:
Cus = (fsc - 0.447fck) Asc
The compressive force in concrete Cuc = 0.362fckbxu
So the total compressive force is given by:
Cu = 0.362fckbxu + (fsc - 0.447fck) Asc
The total tensile force is given by Tu = fst Ast
equating the above two, we get
0.362fckbxu + (fsc - 0.447fck) Asc = fst Ast
From this we get
Eq.12.2
But from Eq.12.1, we can see that fsc depends on xu. So the above Eq.12.2 will not give a closed form solution. We have to use strain compatibility method.
Another point to note is that, fst also depend on xu. If the tension steel has not yielded at ultimate state, we cannot take fst as equal to 0.87fy. So for such sections also, we will have to use strain compatibility method. We will discuss the details of the method when we do a solved example.
It may be noted that the above Eq.12.2 will give a closed form solution if both the tension steel and compression steel have yielded. Because, then fsc and fst will be having a constant value of 0.87fy
Once we determine xu, we can calculate MuR, the ultimate moment of resistance of the doubly reinforced section. For this we will use the compressive forces. We have two compressive forces:
• Cu = 0.362fckbxu. Lever arm of this force = d - 0.416xu. So the contribution from this force = 0.362fckbxu (d - 0.416xu).
• Cus = (fsc - 0.447fck) Asc. Lever arm of this force = d-d'. So the contribution from this force = (fsc - 0.447fck) Asc (d-d')
Sum of the above contributions will be the MuR. So we get:
Eq.12.3: MuR = 0.362fckbxu(d - 0.416xu) + ( fsc - 0.447fck) Asc(d-d')
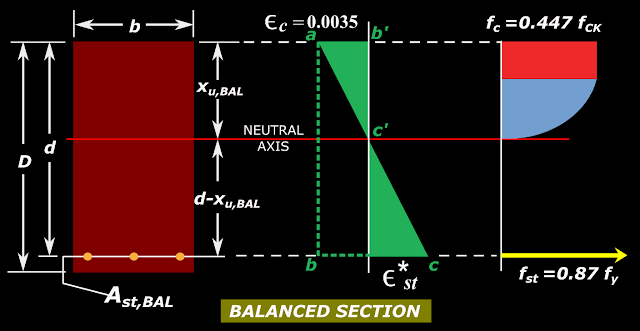
Fig.3.26
Stresses and strains in singly reinforced balanced sections
From the strain diagram in this fig., we saw that xu,Bal, (which is same as xu,max) is the particular depth of NA at which the strain in tension steel is equal to ε*st, the yield strain. If in a beam section, xu is less than xu,max, the strain εst will be greater than ε*st. Then it is an under reinforced section. If xu is greater than xu,max, εst will be less than ε*st. That means the steel will not yield at ultimate state, and it is an over reinforced section.
We can extend the above discussion to Doubly reinforced sections also. As the plane sections remain plane after bending (Details here), the strain diagram for a doubly reinforced section will also be a straight line similar the strain diagram in the above fig. Thus the εst of 'tension steel' in a doubly reinforced section will be greater than ε*st if xu is less than xu,max. It will be less than ε*st if xu is greater than xu,max.
So we can say that while designing a doubly reinforced section, just as in the case of a singly reinforced section, we must ensure that xu is less than xu,max. So that, if over loading occurs, and the beam fails, the failure will be a tension failure.
In the next three sections we will see analysis examples based on the above discussions. Links to these sections are given below.
• Solved example 12.1 • Solved example 12.2 • Solved example 12.3 (over reinforced)
After the above solved examples, a comparison between 'Under reinforced and Over reinforced' doubly reinforced beam sections is given here.
PREVIOUS
We know that when we analyse the section using the Limit State Method, we are calculating the forces in the section at the point of impending failure. The concrete at the extreme compression fibre will be about to crush. And also, if it is an under reinforced section, the steel in the tension zone would have yielded.
So now we are going to find the forces in a doubly reinforced section, at the above mentioned point of impending failure. We can base our discussions on the fig.12.1 given below:
Fig.12.1
Stresses, strains and forces
The above fig. shows all the stresses and forces at the ultimate state. We will now see the details of each component:
The depth of NA is denoted as xu. It's value can be less than or greater than xu,max, depending on the quantities of steel. It is one of our aims to calculate this xu of the given beam section.
We have derived the expression for εsc in the previous chapter. We used the triangles above the NA in the strain diagram. We have the same strain diagram here also. The only difference is that xu,max is now changed to xu. So from Eq.11.1, we get:
Eq.12.1:
The net compressive force in steel is obtained as:
Cus = (fsc - 0.447fck) Asc
The compressive force in concrete Cuc = 0.362fckbxu
So the total compressive force is given by:
Cu = 0.362fckbxu + (fsc - 0.447fck) Asc
The total tensile force is given by Tu = fst Ast
equating the above two, we get
0.362fckbxu + (fsc - 0.447fck) Asc = fst Ast
From this we get
Eq.12.2
But from Eq.12.1, we can see that fsc depends on xu. So the above Eq.12.2 will not give a closed form solution. We have to use strain compatibility method.
Another point to note is that, fst also depend on xu. If the tension steel has not yielded at ultimate state, we cannot take fst as equal to 0.87fy. So for such sections also, we will have to use strain compatibility method. We will discuss the details of the method when we do a solved example.
It may be noted that the above Eq.12.2 will give a closed form solution if both the tension steel and compression steel have yielded. Because, then fsc and fst will be having a constant value of 0.87fy
Once we determine xu, we can calculate MuR, the ultimate moment of resistance of the doubly reinforced section. For this we will use the compressive forces. We have two compressive forces:
• Cu = 0.362fckbxu. Lever arm of this force = d - 0.416xu. So the contribution from this force = 0.362fckbxu (d - 0.416xu).
• Cus = (fsc - 0.447fck) Asc. Lever arm of this force = d-d'. So the contribution from this force = (fsc - 0.447fck) Asc (d-d')
Sum of the above contributions will be the MuR. So we get:
Eq.12.3: MuR = 0.362fckbxu(d - 0.416xu) + ( fsc - 0.447fck) Asc(d-d')
Under reinforced or Over reinforced Doubly reinforced sections
In the case of singly reinforced sections, we have seen the details of 'balanced sections'. We discussed it based on the fig.3.26. This fig. is shown again below:Fig.3.26
Stresses and strains in singly reinforced balanced sections
We can extend the above discussion to Doubly reinforced sections also. As the plane sections remain plane after bending (Details here), the strain diagram for a doubly reinforced section will also be a straight line similar the strain diagram in the above fig. Thus the εst of 'tension steel' in a doubly reinforced section will be greater than ε*st if xu is less than xu,max. It will be less than ε*st if xu is greater than xu,max.
So we can say that while designing a doubly reinforced section, just as in the case of a singly reinforced section, we must ensure that xu is less than xu,max. So that, if over loading occurs, and the beam fails, the failure will be a tension failure.
In the next three sections we will see analysis examples based on the above discussions. Links to these sections are given below.
• Solved example 12.1 • Solved example 12.2 • Solved example 12.3 (over reinforced)
After the above solved examples, a comparison between 'Under reinforced and Over reinforced' doubly reinforced beam sections is given here.
PREVIOUS
