Chapter 17 – Analysis and design of Two way slabs

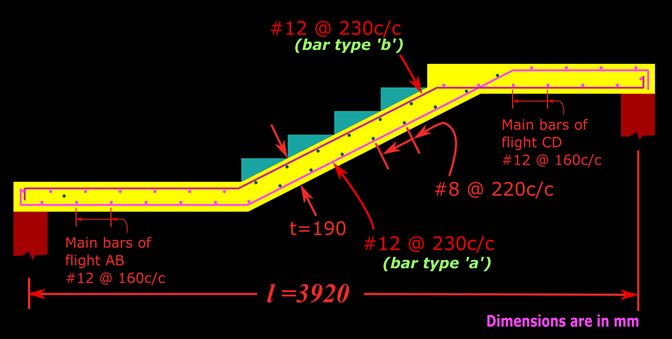
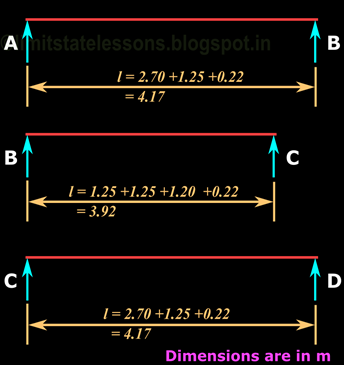
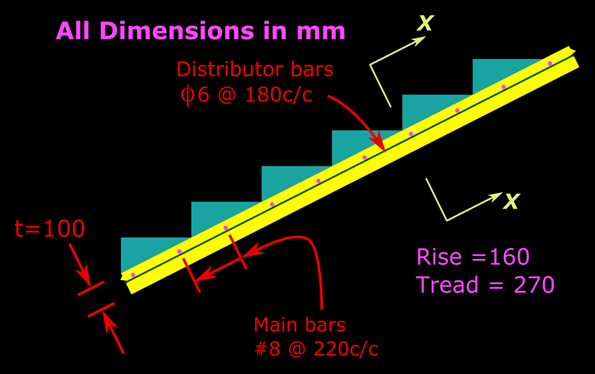
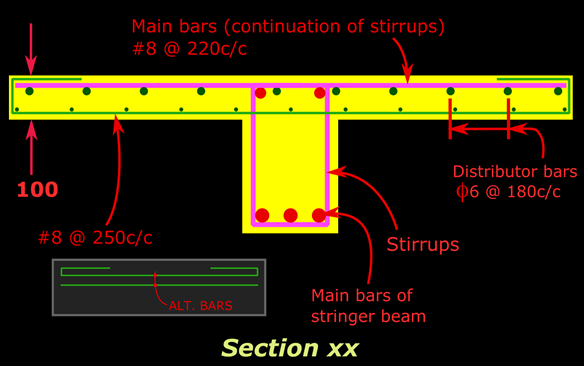
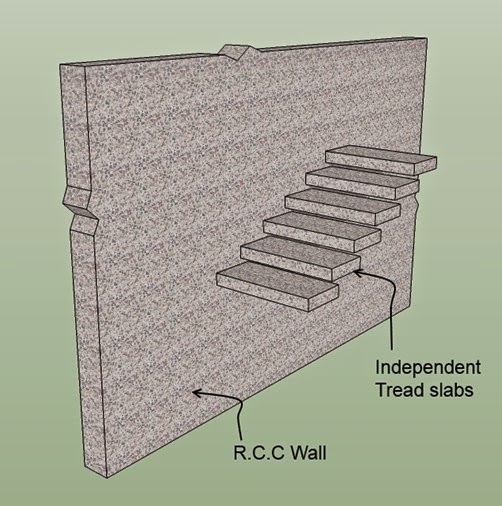
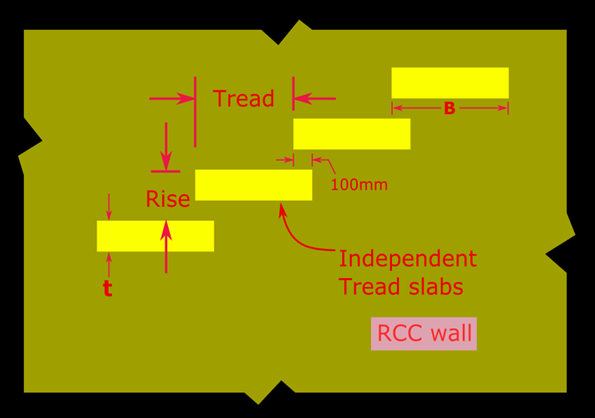
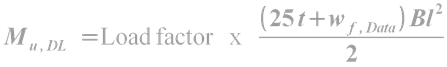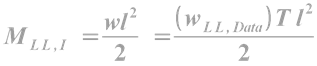At the beginning of Chapter 5- Analysis of One way slabs, we saw a presentation which describes the basic details about the behaviour of Simply supported slabs.  From the presentation, we get a clear understanding about the difference between a one way slab and a two way slab. When the distance l_y increases, more and more load gets transferred in the other (x) direction, and the slab will become more like a one way slab. We have seen the limit beyond which we can design a slab supported on four sides as a one way slab: We take the ratio ly/lx. If this ratio is greater than 2, then we can design it as a one way slab even if it is supported on all the four sides. Here, it is important to note that l_y  is the longer span, and  l_x is the shorter span. This can be made clear based on the following fig.17.1:

Fig.17.1
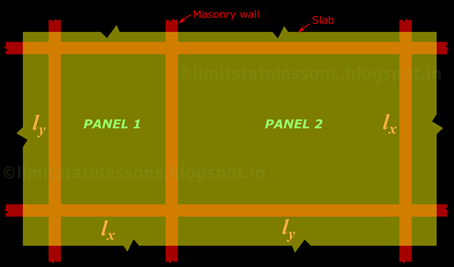
Method of assigning lx and ly
 

In the above fig., the part plan showing the slabs of a building is shown. For panel 1, the shorter span l_x is horizontal and the longer span l_y is vertical. But for panel 2, the shorter span l_x is vertical and the longer span l_y is horizontal. So we must not consider the conventional cartesian coordinate system while denoting the spans of a two way slab. Instead, we must follow the rule: Longer span is l_y and shorter span is l_x . Now we will see some more details about two way slabs:

In a one way slab, the slab is supported on two opposite walls. The loads will be transferred to these two walls only. But when the slab is supported on all the four sides, loads will be transferred to all the four walls. We can think of the total load acting on the slab, to be divided into two unequal shares. One share will be transferred in one direction, and the other share will be transferred in the perpendicular direction. If the slab is a perfect square, both the shares will be equal.

When a slab deflects into a cylindrical surface, there is curvature in one direction only. But when the slab deflects into a spherical surface, at any point on the surface, there is curvature in two mutually perpendicular directions. This means that all elements of the slab will experience a bending in two mutually perpendicular directions. So we must provide steel also in the two directions. The amount of steel that we have to provide in any one of these directions will depend on the bending moment in that direction. This bending moment in turn, will depend on the share of load in that direction. If the slab is a perfect square, then the bending moment in both the directions will be equal. So our next aim is to determine the share in each of the two mutually perpendicular directions.

Before we determine this, let us fix up the notations for the share in each direction, and also the bending moments in each direction. We have fixed up the notations for l_x and l_y based on the fig.17.1 Now we will consider fig.17.2 for loads and bending moments.

Fig.17.2
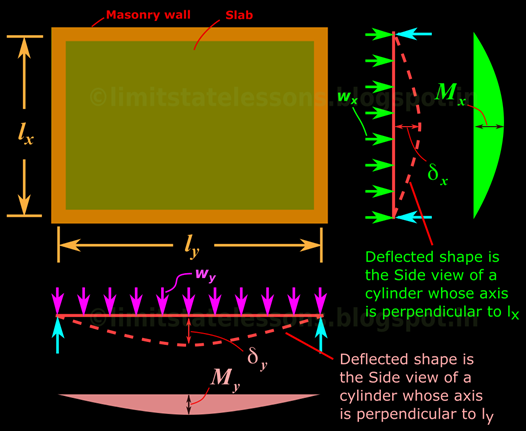
Notations for loads and bending moments

We can think about the bending of a two way slab in this way: The share which is transferred to the shorter walls bends the slab into a cylindrical shape. The share which is transferred to the longer walls also bends the slab into a similar cylindrical shape which is perpendicular to the first cylinder. The combined effect of these two cylindrical bends give the slab a spherical shape. Let us consider the two cylindrical bends separately as shown in the above fig.17.2. If w_y was the only load present, and if the long walls were absent, then the slab will bend into a cylindrical shape, whose axis is perpendicular to l_y. Similarly, If w_x was the only load present, and if the short walls were absent, then the slab will bend into a cylindrical shape, whose axis is perpendicular to l_x. Here w_x and w_y is the uniformly distributed loads over the whole area of the slab. As we will see in later sections, all portions of the slab will not experience the same uniform loads w_x or w_y. But for the ease of analysis, it is convenient to assume it as uniform, for a simply supported two way slab. Thus, from the two deflections shown separately, we can fix up the notations in an 'easy to remember' chart form:

● l_y is the longer effective span, and l_x is the shorter effective span

● The bending moment which makes the cylinder whose axis is perpendicular to l_y is M_y, and the share which causes this Bending moment is  w_y .

● The bending moment which makes the cylinder whose axis is perpendicular to l_x is M_x, and the share which causes this Bending moment is w_x.

Now we can proceed to determine the quantity of these shares. Let us divide the slab into strips parallel to l_x and l_y as shown in the fig. below:

Fig.17.3
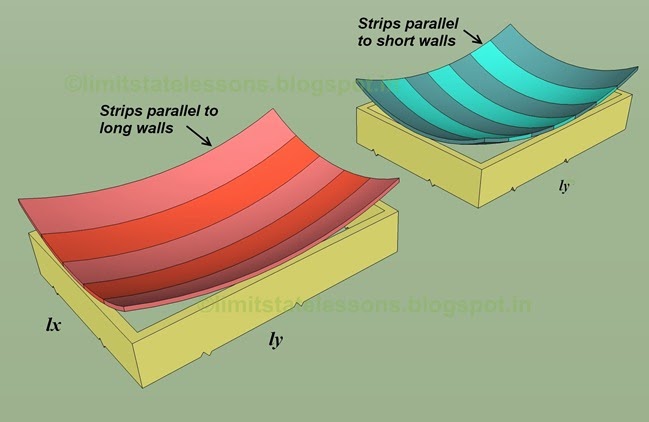
Dividing the slab into strips
 

The red strips are parallel to l_y and the blue strips are parallel to l_x. The width of each of these strips is 1m. In the above fig., the strips are shown in two separate slabs. But actually, both the sets are to be considered in a single slab.

The chart that we prepared above, mentions about a cylinder whose axis is perpendicular to l_y. It also mentions that the share that makes this cylinder is w_y. Now, from the above fig.17.3, we can see that the cylinder whose axis is perpendicular to l_y is made up of strips which are parallel to l_y. So it follows that the share on each strip parallel to l_y is w_y. Similarly the share on each strip parallel to l_x is w_x. As mentioned earlier, w_x and w_y are not distributed uniformly over the whole area. So the load on strips also will not be uniform. Load on each strip will be different from the adjacent strip. We are assuming it to be uniform, for the ease of analysis.  We can add these two points to the above chart and make it complete:

17.1:

● l_y is the longer effective span, and l_x is the shorter effective span

● The bending moment which makes the cylinder whose axis is perpendicular to l_y is M_y, and the share which causes this Bending moment is  w_y .

● The bending moment which makes the cylinder whose axis is perpendicular to l_x is M_x, and the share which causes this Bending moment is w_x.

● The share on each strip parallel to l_y is w_y

● The share on each strip parallel to l_x is w_x

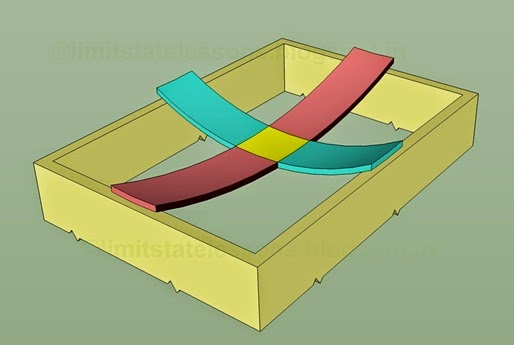
For our discussion, we can take any one strip from each set as shown in the fig.17.4 below:

Fig.17.4
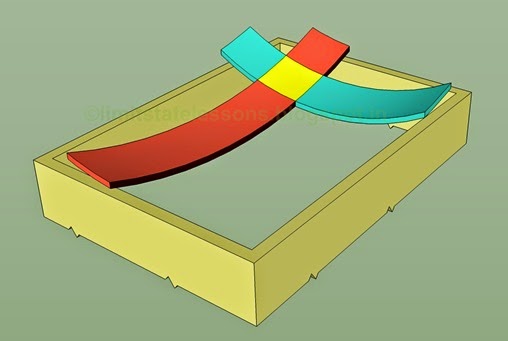
One strip from each set
 

The intersection of the two strips is shown in yellow color. So the yellow portion belongs to both the strips. From the lessons in Strength of materials, we know how to calculate the deflection of a beam at any point. We can consider the red strip and blue strip in the fig., separately. First consider the red strip. If we know the distance to the yellow portion from any of the short walls, we can calculate the deflection of the beam at that portion. Similarly, considering the blue strip, if we know the distance to the yellow portion from any of the long walls, we can calculate the deflection of the blue strip at that portion. The deflection calculated by considering the two different strips should be the same. This is because, which ever strip we consider, the yellow portion has been displaced by the same amount.

The above calculation will be a lot more easier, if we consider the yellow portion to be at the intersection of two ‘central’ strips. This is shown in the fig.17.5 below:

Fig.17.5
Intersection of two central strips
 

In this case, the yellow portion is at the midpoint of each of the strips. The expression for deflection calculation at the midpoint of a beam is a simple one. In the next section we will write this expression for each of the two strips.

PREVIOUS      CONTENTS     NEXT

             Copyright ©2015 limitstatelessons.blogspot.com - All Rights Reserved

Chapter 16 (cont..18)

View previous section

The data available for load calculation are:

R = 150mm, T = 300mm, t= 190mm, w_f,Data = 0.8 kN/m², w LL,Data = 5 kN/m²,
Weight density of the brick masonry for steps = γ_s = 20 kN/m³

Loads on sloping portions:

(1) Self wt. of waist slab =

Eq.16.3

= 5.31 kN/m²

(2) Self wt. of steps =
Eq.16.5
0.5Rγ_s = 1.5 kN/m²

(3) Finishes = 0.8 kN/m²

(4) LL = 5 kN/m²

Total of the four items = 12.61 kN/m²Factored load (Load factor = 1.5) = 18.92 kN/m²

Loads on Landings:

(1) Self wt. of slab =
25t = 4.75 kN/m²

(2) Finishes = 0.8 kN/m²

(3) LL = 5 kN/m²

Total of the three items = 10.55 kN/m²Factored load (Load factor = 1.5) = 15.83 kN/m²

We have discussed the case of right angled stairs on the basis of fig.16.30 There we saw that only half of the load should be taken on the landing of such stairs. Here we have a similar situation. The landing at B is common to flights AB and BC. The load on this landing will contribute to the BM in both the flights. And also, both these flights are independent. That is., they have their own supports. None of them are supported on any landing.

The same situation is present at the landing at C. So we can see that at both the landings, only half the load (15.83 x 0.5 = 7.92 kN/m2) should be considered. Thus we can add loads to the line diagram in the previous fig.105, as shown below:

Fig.16.106
Line diagram showing the loads

We can see that CD is the exact mirror image of AB. So we need to do the analysis and design of AB and BC only. The design of AB can be applied to CD also.

First we will analyse AB:

Eq.16.11:

Eq.16.12:

 

The following data is available to us for using in the above equations:

w₁ = 18.92 kN/m, w₂ = 7.92 kN/m, l₁ = 2.81 m, l₂  = 1.36 m

So we get R_A = 37.01 kN  and  R_B = 26.93 kN

The Bending moment at any point at a distance x from the support A is given by:

Eq.16.13:

If we differentiate this equation, we will get the equation for the shear force at any point at a distance x from the support A:

Eq.16.14

The maximum bending moment occurs at a point where the shear force is equal to zero. So we equate the above equation 16.14 to zero and solve for x

Thus we get x = 1.96m from support A

Substituting this value in Eq.16.13, we get Maximum bending moment = 36.2 kNm

Thus we determined the reactions and bending moment in flight AB. Now we will analyse BC:

Reactions at supports B and C is given by

Eq.16.15:

 

The following data is available to us for using in the above equations:

w₁ = 18.92 kN/m, w₂ = 7.92 kN/m, l₁ = 1.2 m, l₂  = 1.36m

So we get R_B = R_C = 22.12 kN

The maximum bending moment occurs at midspan and is given by

Eq.16.16

= 26.17 kNm.

Thus we determined the reactions and bending moment in flight BC also. So now we can design the steel and do the various checks. The design part is given as two separate pdf files the links of which are given below:

Design of Flight AB

Design of Flight BC

The reinforcement details according to the above designs are shown in figs.16.107,108 and 109 below:

Fig.16.107
Reinforcement details of flight AB

Fig.16.108
Reinforcement details of flight BC

Fig.16.109
Reinforcement details of flight CD

The bar diameters and their spacing in the last flight CD will be same as that of the first flight AB. But the bending of the bars at the supports is different for the two flights. So they are shown separately.

The second flight BC does not require distributor bars in the landings B and C. This is because the main bars of flights AB and CD will act as distributors. So we need to provide distributor bars for BC in it’s sloping portion only.

It should be noted that the main bars of the two flights AB and CD pass above the main bars of BC. Flight BC is not required to carry the loads from the other flights. But even then it’s bars are given beneath the others. This is because it is always better to give the bars of the shorter span as the bottom most layer.

This completes the analysis and design of the open well staircase. In the next chapter we will discuss about the design of Two way slabs.

PREVIOUS      CONTENTS     NEXT

             Copyright ©2015 limitstatelessons.blogspot.com - All Rights Reserved

Chapter 16 (cont..17) Design of Open well staircase

In this section we will discuss the analysis and design of an 'Open well stair'. In this type of stairs, the flights and landings used for climbing, are given near the outer walls of a stair case room. This will create a 'well-like' portion near the middle of the room. The figs.16.102,103 and 104 below shows the plans and sections of an open-well stair.

Fig.102
Key plan showing position of beams, columns and the staircase

Fig.103
Section XX

Fig.104
Section YY

In the above figs., the method of naming of beams and columns is as specified in SP34. For example: COL 2 Q₂ is the column Q₂ in FLOOR 2.

From the key plan, we can see that in each floor, there are three flights. AB, BC and CD. In Floor1. the flight AB rests on the ground at A and on an inclined beam at B. This inclined beam (denoted as S_t,B) is supported on Col Q1 and Q2. Flight BC is supported on masonry walls at B and C. Though not related to our present stair design problem, lintel beams should be provided in all the masonry walls as shown in the section YY. In this building, the height at which landing C is embedded in the masonry wall coincides with the position of the Lintel beam.  Flight CD is supported on the inclined beam S_t,B at C and on beam B_m4 at D. The same arrangement is provided in Floor 2 also. The only difference is that the flight AB starts from the beam. The part views of the building can be seen in the slide show below:

We will do the analysis and design of the three flights in Floor2. For this first we will draw the line diagram of each flight showing the effective spans. This is given in the fig.105 below:

Fig.105
Effective span of flights

From the fig.105, we can see that AB and CD have the same effective span,and has the largest value of 4.17m. So we will use this value to fix up the preliminary value of 't', the thickness of waist slab. For all the previous problems on longitudinal stairs, we used the thumb rule of t = l /20 to fix up a preliminary value. Now we will see a different method:

From the previous examples, we have seen that, a lower value of thickness may be sufficient to resist the bending moment, but that lower value will not satisfy the deflection check. That is., the deflection criterion is more important than the bending moment criterion, when finalising the thickness of the slab. So we will do the procedure for deflection check in a sort of 'reverse' manner to fix up a preliminary value for 't'. This can be done as follows:

We know that, for spans less than 10m, to satisfy the deflection check, the following condition should be satisfied: (Details here)

   - - - - (1)

For simply supported members, (l/d) basic = 20.

Now we take k_t. This can be calculated by using the expression given in SP24:

  - - - - (2)

where

    - - - - (3)

But in the above expressions, there are three unknowns. (a) p_t, (b) Area of steel required, and (c) Area of steel provided. These three unknowns can be solved by making two simple assumptions.

First we assume the Area of steel provided for a 1m wide strip with total depth t = 200mm. If the concrete cover  is 20mm, and 12mm (Fe 415) bars are provided, effective depth d = 200 –20 –6 = 174mm:

Assume that 12 mm bars are provided at a spacing of 150mm c/c. So we can make the bar area calculations (Details here):

=113.1 mm²

= 754 mm²  - - - - (4)

So p_t = (A_st x 100) / (b d) = (754 x100)/(1000 x174) = 0.43% - - - - (5)

So we can say that the p_t for a stair will have a value around 0.43%. It may be noted that 0.43% is only an approximate value. In some stairs it can go up to 0.50% or even more. But the next time we do a problem of longitudinal stairs, we can straight away assume p_t  = 0.43%. There is no need to assume a section and the steel provided, and do the area calculations above.

However, this is only for preliminary dimensions.  The dimensions so obtained should be finalised only after detailed checks using the actual value of steel required and steel provided.

Now we assume that the Area of steel required is same as the Area of steel provided = 754 mm² 

So f_s will become 0.58 x f_y = 0.58 x415 = 240.7 - - - - (6)

Substituting (5) and (6) in (2), we get k_t = 1.3 - - - - (7)

Substituting (7) in (1) we get (l/d) provided should be less than or equal to 20 x 1.3 = 26

In our present problem, l = 4170mm

So 4170 /d ≤ 26

So d should be greater than or equal to 4170/26 = 160.4 mm

If d is to be greater than 160.4mm, t should be greater than 160.4 +6 +20 = 186.4mm - - - - (8)

If we use the thumb rule we will get total depth t = 4170/20 = 208.5mm - - - - (9)

Let us adopt the value in (8) and provide t = 190mm.

However, as mentioned above, the design using this value of 190mm should be finalized only after the checks using actual area of steel required and the actual area of steel provided.

For a uniform appearance, we can provide the same t for flight BC also. Thus, the load per 1m² area will be same on all the flights. We will see the load calculation details in the next section.

PREVIOUS      CONTENTS      NEXT

             Copyright ©2015 limitstatelessons.blogspot.com - All Rights Reserved

Chapter 16 (cont..16)

The following solved example illustrates the design of a typical structurally independent tread slab of a stair

Solved example 16.6 

The reinforcement details according to the above solved example is shown in the fig.16.97 below:

Fig.16.97
Reinforcement details

We will now discuss about the above fig.
In cantilever members, the main tensile steel is given at the top. So in our case, the main bars are given as the top most layer. The distributor bars are given as the second layer from the top. This arrangement will give maximum possible effective depth ‘d’ for the section.

The 10 mm dia. main bars at the top should be given sufficient anchorage. This is obtained by giving a standard 90^o bend, and extending each of them into the wall. The length of this extension from the face of the wall should be determined:

Details about development length can be seen here: unique value of Ld

(a) The 10mm dia. bar that we are considering is mild steel and so they are not deformed
(b) The bar is in tension
(c) The grade of concrete is M20

From (c) above, we get  τ _bd  = 1.2 N/mm². From (a), the bar is not deformed. So we cannot increase this τ _bd  by 60%. Substituting the values in Eq.14.6 we get L_d  = 453 mm. So each of the 10 mm dia. main bars at the top should be given an extension which is not less than 453 mm.

As the slab has a thickness of 100 mm, a bottom layer consisting of 3 Nos. of 8 mm mild steel bars should be given. This is indicated by the green bars at the bottom layer in section XX. These 3 bars should be given two 90 degree bends at the free end. This is for tying them with the top layer. Distributor bars for this layer consists of 5 Nos. of 6mm mild steel bars. These 3 bars at the bottom most layer also take up loads when stress reversal occurs when the slab is subjected to seismic loads. So these bars should also be given extension into the wall.

In this type of stairs with independent tread slabs, a vertical gap will be present between adjacent slabs. It is recommended that this gap should be filled up with materials of low density such as Light weight concrete, before applying cement plaster or laying tiles. This filling is done in the overlapping 10cm. So the ‘Tread’ of the slabs will not be reduced. This is shown in the fig.16.98 below. As this is done before the finishing works, the use of a different material for the filling will not be visible afterwards.

Fig.16.98
Filling of the vertical gap
 

Structurally independent tread slabs simply supported at ends

Fig.16.99
Part view of a stair

The above fig. shows the part view of a stair. It consists of independent tread slabs. These slabs are simply supported on masonry walls on either sides of the stair. This type of stair is used only for climbing small heights of about 45 cm to 100 cm. This is because, for climbing higher, the walls on either side will have to be built higher. When climbing higher, the length of stair and the walls will also increase, and this will lead to loss of space under the stair.

The Rise, Tread, and other details are same as that we saw earlier in fig.16.90 in a previous section

The design of a typical tread slab of this type of stair is easier than that of a cantilevering tread slab because alternate Live loads need not be considered. But all other load calculation procedure are the same.

So the three items that constitute the load on 1m length of the tread slab are given by Eq.16.26, 27 and 28. Thus we can write:

Eq.16.34
The load per meter length of a tread slab simply supported on walls = w₁ = Eq.16.26 +27 +28

When w₁ is determined, we can draw the line diagram as shown below:

Fig.16.100
Line diagram for analysis

From this, we will get the maximum Bending moment at the midspan, and the design of reinforcement can be done. For preliminary proportioning, a thickness of 80mm can be assumed for span upto 1m.

The following Solved example illustrates the design of a typical structurally independent tread slab supported on masonry walls on either side of the stair.

Solved example 16.7

The reinforcement details according to the above solved example is shown in the fig.16.97 below:

Fig.16.101
Reinforcement details

In the above fig., we can see that the main bars are given in the bottom most layer. They are given a 90^o bend at both ends. This bend give better anchorage for the bars.

It may be noted that in this type of stairs also, it is better to fill up the vertical gap between adjacent tread slabs, as we saw earlier in fig.16.98 above.

We have seen the commonly used types of stairs in the above discussions. Before moving to the next chapter, which is about Two way slabs, we will discuss about the design of a ‘Open well staircase’ in the next two sections.

PREVIOUS      CONTENTS      NEXT

              Copyright ©2015 limitstatelessons.blogspot.com - All Rights Reserved

Chapter 16 (cont..15)

For doing the analysis and design, we must first calculate the loads acting on any one slab. For slabs, we usually take the load on 1 m² area, and when we consider a strip of 1m width, this will be the load per meter length of the strip. But in our present case, we cannot take a 1m wide strip because the width ‘B’ of the tread slab is less than 1m. The area on which the load is to be calculated is shown in green colour in the fig.16.91 given below:

Fig.16.91
Plan showing area of the slab on which load is taken

Self wt. of tread slab:
The area of the green coloured portion = 1 x B = B m²
Thickness perpendicular to the plane of the paper = 't'm
So volume = Bt m³
Unit wt. of RCC = 25 KN/m³
Thus wt. of the green coloured portion = 25Bt kN
This is the self wt. on 1m length of the slab.
So we can write:

Eq.16.26
Self wt. of tread slab = 25Bt kN/m

Wt. of finishes:
This is obtained from the codes or data books. It is specified as load per 1m² of horizontal area. But we are having an area, which though is horizontal, have a lesser value (1 x B m²= Bm²) than 1m². So we have to modify the value that we obtain from the code or data book, by multiplying it with the actual area that we have. So, if we denote the value obtained from the data book as w_f,data then we can write:

Eq.16.27
Wt of finishes = w_f,data x B kN/m

Live load:
This is also obtained from the codes or data books. It is specified as load per 1m² of horizontal area. But we are having an area, which though is horizontal, have a lesser value than 1m². In the case of LL, the area that we have is still lesser than B m² because the LL will not be applied on the overlapping area. This is shown in the fig.16.92 below:

Fig.16.92
Lesser area on which LL act

Thus the area that we have is T m². So we modify the value that we obtain from the code or data book, by multiplying it with the actual area that we have. If we denote the value obtained from the data book as w_LL,data then we can write:

Eq.16.28
LL = w_LL,data x T kN/m

If we sum up the above three items, we will get the total load acting per 1m length of the slab. But we have to do one more step in this type of stairs. We have to consider another type of LL as specified by the loading code. Accordingly, each tread slab should be capable to resist a concentrated load of 1.3 kN acting at the free end as shown in the fig. below:

Fig.16.93
Concentrated load at the end of cantilever

These two Live loads can be considered separately. That is., we can assume that they do not act at the same time. So we have to consider two possible line diagrams as shown in the figs. below:

Fig.16.94
Uniformly distributed DL and LL

Fig.16.95
Uniformly distributed DL and concentrated LL

Out of the above two cases, the one which gives the maximum bending moment at the support must be considered for analysis and design.

The expression for calculating the bending moment caused by a concentrated load is different from that for a UDL.

BM at the support of a cantilever due to UDL = w l² /2

BM at the support of a cantilever due to concentrated load at free end = Wl

So we have to consider these loads separately. The procedure can be summarized as follows:

First we calculate the BM due to the self weights (DL) based on Eqs. 16.26 and 27

Multiplying this by the Load factor, we will get the factored BM. So  we can write:

Eq.16.29:

This is a final quantity, and will not change because we are not considering any other types of DL.

Now we calculate the BM due to the usual LL based on Eq.16.28. We will call it as ‘type I’ LL.

Multiplying this by the Load factor, we will get the factored BM. So  we can write:

Eq.16.30:

Next we calculate the BM due to the concentrated LL. We will call it as ‘type II’ LL.

Multiplying this by the Load factor, we will get the factored BM. So  we can write:

Eq.16.31:

Next we add the two LL moments  to the DL moment separately, to get the two possible Bending moments that can occur. So we can write:

Eq.16.32:

Sum₁= M_u,DL  + M_u,LL,I  
Sum₂= M_u,DL  + M_u,LL,II   

Out of the above two sums, the largest one is our required value.

The above steps can be represented by a simple flow chart as shown below:

Fig.16.96
Flow chart for final Bending moment

Thus we get the final factored bending moment, which can be used for the design.

In a similar way, the shear force at the support can also be calculated. The two possible alternative Live loads should be considered, and the one which gives the maximum effect should be taken for the design. For a cantilever member, the reaction at the support is simply equal to the total load on the member. So we can write:

Eq.16.33

Sum₁= (w_u,DL  + w_u,LL,I ) l

Sum₂= (w_u,DL  ) l+ w_u,LL,II 

Out of the above two sums, the largest one is our required value.

In the above equation,
w_u,DL = Load factor x (25t + w_f,Data)B Based on Eq.16.26 and 27
w_u,LL,I = Load factor x (w_LL,Data)T Based on Eq.16.28

w_u,LL,II = Load factor x 1.3 Based on Fig.16.93

So we are now in a position to design a typical tread slab of this type of stair.

For preliminary proportioning of the slab, value of ‘t’ can be assumed to be approximately equal to l /10. But it should be finalized only after the required checks.

In the next section, we will see a solved example based on the above discussion.

PREVIOUS      CONTENTS      NEXT

             Copyright ©2015 limitstatelessons.blogspot.com - All Rights Reserved