Chapter 3 (cont..8) Depth of Neutral axis of Under reinforced and Over reinforced sections

In the previous section we saw that the principle of similar triangles cannot be used for calculating the depth of NA of Under reinforced sections and Over reinforced sections. In this section we will see the alternate methods.

In the method of similar triangles, we used the triangles in the strain diagrams. Let us now take the stress diagrams and the forces. The stresses in an Under reinforced section is shown in fig.3.29 below: This is the first row in fig.3.25. In it, forces are also shown now for better understanding.

Fig.3.29
Forces in an under reinforced section at ultimate state 

The net compressive force C_u is acting at the centroid of the compressive stress block. This centroid is at a distance of 0.416x_u,U from the top most compression fibre. (Details here). We have calculated the magnitude of C_u also. It is given by Eq.3.7

Eq.3.7
C_u = 0.362f_ck b x_u,U

The tensile force in steel is given by: [stress in steel x Area of steel]. We know that the steel in an Under reinforced section would have yielded at ultimate state, and so the stress in it is constant at a value of 0.87f_y. So the force in steel is given by

Eq.3.16
T_u = 0.87f_y A_st,U 

For equilibrium,  C_u must be equal to T_u. So we can equate 3.7 and 3.16.

From this we get 0.362f_ck b x_u,U = 0.87f_y A_st,U 

Thus we get 
Eq.3.17

In this equation, all quantities on the right are known, and so we can compute x_u,U. If this x_u,U is less than x_u,BAL of the section, we can confirm that it is an under reinforced section. Also, once we obtain x_u,U, we can determine all other important quantities like total compressive force C_u, centroid of the compressive stress block etc.,

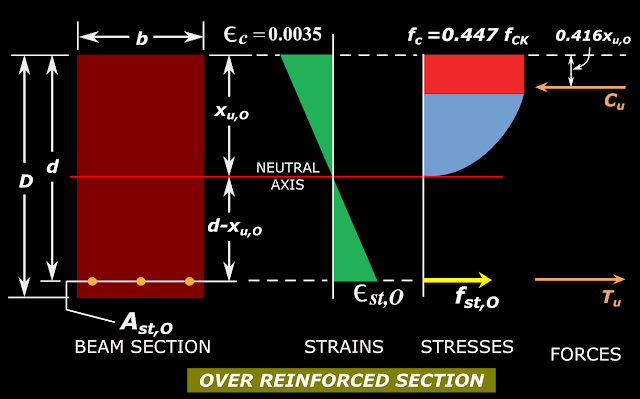
Now we will try to find x_u,O, the depth of NA for an over reinforced section. As in the case of an under reinforced section, here also we will draw the stress diagram and the forces.

Fig.3.30
Forces in an Over reinforced section at ultimate state

C_u = 0.362f_ck b x_u,O

T_u = (f_st,O)(A_st,O) 

As before, we equate C_u and T_u to get
Eq.3.18

Here, f_st,O is NOT a known quantity. We know the reason for this: In an over reinforced section, the steel would not have yielded at the ultimate state. So the stress has not reached the horizontal magenta region of the stress strain curve of steel. It is still in the blue curve or the initial red line.

But if we can find the strain in steel, we can find the stress from the design curve. For finding the strain, we must use the strain diagram. In the previous section, we used the strain diagram of an over reinforced section and obtained Eq.3.15

Eq.3.15

We want the strain. So let us bring it to the left side:

Eq.3.19

In the above equation, we find that the strain ε_st,O depends on x_u,O the depth of NA . So the steps that we did so far can be summarized as follows:

• We started out to find x_u,O the depth of NA of an over reinforced section. 
• For that, we want to know the stress f_st,O in steel. 
• For finding this stress, we want to know the strain ε_st,O. 
• But the strain ε_st,O depends on x_u,O the depth of NA.

This forms a loop as shown in the fig. below:

It will not give a solution. So we must use an iterative method.

This iterative method is commonly known as Strain compatibility method.

The steps involved in this method to find x_u,O are the following:

1. We first assume x_u,O, the depth of NA to be at a particular trial value. With that, we are dividing the beam section into an upper part and a lower part. 
2. Determine the compressive force C_u in the upper part. 
3. Determine the Tensile force T_u in the lower part. 
4. For equilibrium, C_u must be equal to T_u. 
If they are equal, the assumed value of x_u,O is correct. If they are not equal, we repeat the steps using a new improved value of x_u,O. We repeat the steps until C_u becomes equal to T_u.

The above steps will be clear when we see a solved example. First we will see a simple problem of the 'analysis of an under reinforced section':

Solved example 3.1

Next we will see the solved example of the 'analysis of an over reinforced section'. This will require iteration process using 'strain compatibility'.

Solved example 3.2
Determine the depth of Neutral axis x_u at the ultimate state for the beam section shown below. Given b =230 mm, d =400 mm, A_st =1119.19 mm², f_y =415 N/mm², f_ck =20 N/mm²

Solution:
So we are going to analyse the given beam section to find the stresses, strains, forces and x_u, depth of NA at the ultimate state. We will see the various steps involved in the analysis in detail:

Initially, we assume that 'the tension steel will yield at the ultimate state'. 

We will now check if this really happens at the ultimate state. For making this check, first we find x_u the depth of NA. We have assumed that the tension steel has yielded. So the stress in tension steel =0.87f_y. Thus the force in tension steel =T_u =0.87f_yA_st = 0.87 x 415 x 1119.19 =404083.55 N

Force in concrete = C_u = 0.362f_ckbx_u,U = 1665.2x_u,U

Equating the tensile and compressive forces we get: 1665.2 x_u,U = 404083.55 N - - - (1) 

So we get x_u,U = 242.66 mm - - - (2)

We can also use Eq.3.17 directly:

Eq.3.17

We know how to calculate the strain ε_st from the strain diagram. The equation  is Eq.3.14 :


Rearranging this we get

Note that we are using the equation for ε_st,u because we have assumed that the tension steel has yielded. Using this equation we get ε_st = 0.00227.

Now we compare the values with the yield strain ε*_st. We know that, for Fe415 steel, ε*_st = 0.00380. Comparing the values, we find that ε_st < ε*_st. 

[There is another method to prove that ε_st is less than ε*_st: We know that, if x_u ≤ x_u,max, the tension steel would have yielded. In our case x_u,max =0.4791 x 400 =191.64 mm. In the above calculations, we have used x_u =242.66 which is greater than x_u,max. So for this value of x_u, the steel would not yield, and so, ε_st will indeed be less than ε*_st.]

So, if at the ultimate state, the NA is at the position x_u = 242.66 mm, the tension steel would never yield. This means that:
• The stress in A_st is not 0.87f_y
• The section is an 'Over reinforced one'
So the equality in (1) is not valid. Thus the value of x_u = 242.66 mm is not correct.

As it is an over reinforced section, we have to use iteration method using strain compatibility. We want an improved value of x_u. We will try to obtain the new value, based on the value that we are having.

In the fig above, 'Line p' shows the position of the NA when x_u = x_u,max =191.64 mm. The NA of our beam section will never occupy this position because, it is an 'Over reinforced section', and so x_u will be greater than x_u,max.. The other 'Line q' shows the position when the tension steel has yielded. This position will also never occur because an over reinforced section will fail (by compression of concrete in the extreme fibre) before the yielding of it's tension steel occurs. The actual NA lies some where between these two lines. So we can take the average of these two values as the initial 'trial value'. Thus x_u for the 1^st cycle = 0.5 x(191.64 +242.66) =217.17 mm.

Cycle 1:
When the NA is in the position x_u =217.17, ε_st is obtained using Eq.3.15 : 

Rearranging this we get:

[The equation involving x_u,o and ε_st,o is used here because the section is over reinforced. But it may be noted that Eq.3.14 and 3.15 are the same with only the subscripts changed from 'u' to 'o'.]

So we will get ε_st =0.002947. The corresponding stress f_st is obtained from the table for Fe 415 steel:
0.002760  → 351.800
0.002947  → 353.430
0.003800 → 360.900. So we get f_st =353.43 N/mm². With this stress value, we can calculate the forces:

C_u = 0.362f_ckbx_u = 1665.2 x217.17  = 361623.87 N

T_u =f_stA_st =343.430 x1119.19 = 395560.2 N

These forces are not equal. So we don't have an equilibrium. What is the value of x_u if 343.430 was indeed the stress? We can calculate this by writing the equality: C_u = T_u. Thus we write:

1665.2 x_u = 395560.2.

From this we get = x_u =237.55 mm. We will take the average of this x_u and the value of x_u used in this cycle. It is equal to 0.5 x(217.17 +237.55) =227.36 mm. This can be used as the trial value for the next cycle.

Cycle 2:
When the NA is in the position x_u =227.36, ε_st is obtained using Eq.3.15 . 

So we will get ε_st =0.002658. The corresponding stress f_st is obtained from the same table for Fe 415 steel:
0.002410  → 342.800
0.002658  → 349.170
0.002760 → 351.800. So we get f_st =349.17 N/mm². With this stress value, we can calculate the forces:

C_u = 0.362f_ckbx_u = 1665.2 x227.36  = 378592.04 N

T_u =f_stA_st =349.17 x1119.19 = 390789.57 N

These forces are not equal. So we don't have an equilibrium. What is the value of x_u if 349.17 was indeed the stress? We can calculate this by writing the equality: C_u = T_u. Thus we write:

1665.2 x_u = 390789.57.

From this we get = x_u =234.68 mm. We will take the average of this x_u and the value of x_u used in this cycle. It is equal to 0.5 x(227.36 +234.68) =231.02 mm. This can be used as the trial value for the next cycle.

Cycle 3:
When the NA is in the position x_u =231.02, ε_st is obtained using Eq.3.15 . 

So we will get ε_st =0.002560. The corresponding stress f_st is obtained from the same table for Fe 415 steel:
0.002410  → 342.800
0.002560  → 346.660
0.002760 → 351.800. So we get f_st =346.66 N/mm². With this stress value, we can calculate the forces:

C_u = 0.362f_ckbx_u = 1665.2 x231.02  = 384690.81 N

T_u =f_stA_st =346.66 x1119.19 = 387980.05 N

These forces are not equal. So we don't have an equilibrium. What is the value of x_u if 346.66 was indeed the stress? We can calculate this by writing the equality: C_u = T_u. Thus we write:

1665.2 x_u = 387980.05.

From this we get = x_u =232.99 mm. We will take the average of this x_u and the value of x_u used in this cycle. It is equal to 0.5 x(231.02 +232.99) =232.01 mm. This can be used as the trial value for the next cycle.

Cycle 4:
When the NA is in the position x_u =232.01, ε_st is obtained using Eq.3.15 . 

So we will get ε_st =0.002534. The corresponding stress f_st is obtained from the same table for Fe 415 steel:
0.002410  → 342.800
0.002534  → 346.000
0.002760 → 351.800. So we get f_st =346.00 N/mm². With this stress value, we can calculate the forces:

C_u = 0.362f_ckbx_u = 1665.2 x231.02  = 386335.43 N

T_u =f_stA_st =346.00 x1119.19 = 387237.61 N

These forces are not equal. So we don't have an equilibrium. What is the value of x_u if 346.00 was indeed the stress? We can calculate this by writing the equality: C_u = T_u. Thus we write:

1665.2 x_u = 387237.61.

From this we get = x_u =232.55 mm. We will take the average of this x_u and the value of x_u used in this cycle. It is equal to 0.5 x(232.01 +232.55) =232.28 mm. This can be used as the trial value for the next cycle.

Cycle 5:
When the NA is in the position x_u =232.28, ε_st is obtained using Eq.3.15 . 

So we will get ε_st =0.002527. The corresponding stress f_st is obtained from the same table for Fe 415 steel:
0.002410  → 342.800
0.002527  → 345.820
0.002760 → 351.800. So we get f_st =345.82 N/mm². With this stress value, we can calculate the forces:

C_u = 0.362f_ckbx_u = 1665.2 x232.28  = 386786.52 N

T_u =f_stA_st =345.82 x1119.19 = 387035.07 N

These forces are close to each other. So we have an equilibrium. The value of x_u can be taken as 232.28 mm

In the next section we will see more properties of beam sections.

PREVIOUS

NEXT

                    

            Copyright ©2015 limitstatelessons.blogspot.com- All Rights Reserved