In the previous section we discussed about the bond stress between concrete and steel. We saw the importance of providing the required development length. We did our discussions based on a cantilever beam. Now we will see some other situations.
Consider a doubly reinforced cantilever beam as shown in fig.14.5 below:
In the previous section, we have seen how the top steel in the above beam can be made safe from being pulled out. Now we will see the bottom steel. The bottom steel is in compression. So they will be pushed in. The concrete should have sufficient grip on the bar for preventing this from happening. For this, there should be sufficient embedded length. Here the required embedment is the Ld for compression steel. We can calculate it using the same Eq.14.6 used for tension steel. The only difference is that, if deformed bars are being used, we must increase the bond stress in table 14.1, first by 60 per cent, and then by 25 per cent.
Next we consider a situation encountered in a simply supported beam. Fig.14.6 shows the region near the left support of a simply supported beam carrying a UDL. The bending moment diagram is also shown.
Fig.14.6
Simply supported beam carrying a UDL
The beam is reinforced with 2 types of bars – bar 'a' and bar 'b' . Bar 'a' continues uninterrupted from one support to other. But bar 'b' is curtailed at section AA. This is because the bending moment is decreasing progressively towards the support, and so all the bars provided near the midspan region need not be provided at the regions near supports. We can find the section AA beyond which bar 'b' is no longer required. We will discuss the method to determine the position of AA in a later section. At present we are more concerned about another matter:
We cannot cut off the bar 'b' at the exact section AA as shown in the above fig. The reason is as follows: We know that bar 'b' is carrying tensile loads. That means it is being stretched. So it will have a tendency to regain it's original length, and so it will try to shorten. It will try to shorten back to it's original length. If this shortening happens, it will mean that the end of the bar is moving away from section AA, towards the mid span region of the beam. So the bar will no longer be available at AA. To prevent this from happening, we must extend the bar 'b' even beyond AA to a certain distance as shown in fig.14.7 below. This distance should be such that, it is sufficient for the concrete to exert the required grip on the bar, to prevent it from shortening back to it's original length. In other words, the bar 'b' must be given sufficient ‘anchorage’ beyond section AA.
Fig.14.7
Extension of the bar
Curtailment of bar is done for economy in the design. In addition to the above discussed points, some other aspects also have to be considered while doing bar curtailment. So we will discuss about them as a separate topic in a later section.
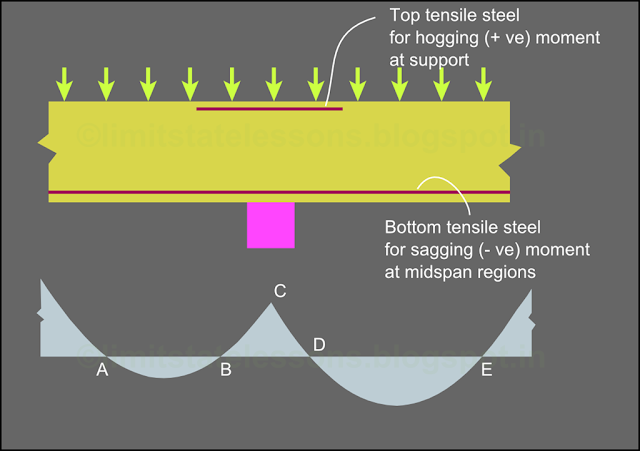
Next we look at a portion of a continuous beam shown in fig.14.8. Here top tensile steel is provided for the hogging moment at the support, and bottom tensile steel is provided for the sagging moment at midspan regions. (A video demonstrating the requirement of top bars at continuous supports can be seen here)
Fig.14.8
Continuous beam carrying UDL
From the bending moment diagram, we can see that the hogging moment progressively decreases on either sides of the support (Value at C decreases towards B on the left side, and towards D on the right side). This indicates that the steel provided for this moment can be curtailed at some distance away from the support. But while doing this curtailment, we must take care of the anchorage requirements beyond the section.
The same is true for the bars provided for the sagging moments also in such continuous beams. As we move from the midspan regions towards either supports, the sagging moment progressively decreases. So here also curtailment can be used for economy, provided anchorage requirements are satisfied.
Yet another point that we have to consider in the above fig. is the bar arrangement related to the points of inflection. In the fig., A,B,D and E are points of inflection. The moments change signs at these points. The bottom steel provided for the region between A and B is not required in the region from B to C, because there, the moment is changing signs from – ve to + ve. But we cannot stop the bars at exact A or B. Anchorage and other requirements like shear, prevention of cracks etc., that are specified by the code should be satisfied.
As mentioned earlier, we will discuss about them as a separate topic ‘curtailment of bars’ in a later section. At present, we have obtained an understanding that anchorage and development length requirements is one of the many important points that have to be considered while finalizing the arrangement of bars in a structural member. We will now focus our attention on the other aspects of bond and development length.
Development length of bundled bars
In the case of bundled bars, the development length required will have a higher value than individual bars. This is because, when bars are bundled together, the area of contact between each bar and the concrete will be reduced. So the grip that concrete exert on the steel will also be reduced. This can be compensated by providing a greater development length, so that more portion of steel will come in contact with the concrete. The quantity by which the length has to be increased is specified by the code:
When two bars are in a bundle:
• First calculate the Ld for a single bar.
• Then increase this Ld by 10 per cent. That is., new 'increased Ld' = Ld x1.1
• Give this increased Ld for each of the two bars in the bundle.
• First calculate the Ld for a single bar.
• Then increase this Ld by 10 per cent. That is., new 'increased Ld' = Ld x1.1
• Give this increased Ld for each of the two bars in the bundle.
When three bars are in a bundle:
• First calculate the Ld for a single bar.
• Then increase this Ld by 20 per cent. That is., new 'increased Ld' = Ld x1.2
• Give this increased Ld for each of the three bars in the bundle.
In a similar way, when there are 4 bars in a bundle, the increase must be 33 per cent. This method of increment can be diagrammatically represented as shown in the fig. below:
Development length for bundled bars
Development length when area of steel provided is greater than area of steel required
As we have seen in the design of beams and slabs, the calculated area cannot be given as such. Bars are available only in certain diameters. We have to choose the proper combination of bar diameters and the number of bars to get the required area. And care should be taken to see that area provided is not less than the area required. This will usually result in an upward rounding. That is., the area provided will usually be greater than area required. In such situations we can provide a modified value of development length denoted as Ldm. The expression for obtaining Ldm given in clause 25.2.1 of SP 24 is shown below:
Eq.14.7
So we first determine Ld as usual, and multiply it by the ratio (As,required / As,provided).
In the next section we will discuss about bends, hooks etc., that are given to bars for improving anchorage.





No comments:
Post a Comment