Chapter 15.10 - Curtailment of bars in frames

In the previous section we saw the lengths of bars and areas of bars that have to be embedded at a simple support and at a continuous support. These requirements are given in the sub clause (a) of 26.2.3.3.

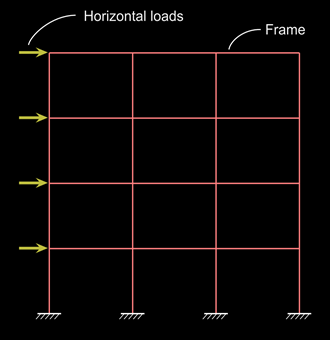
Now we will see the next sub clause: cl.26.2.3.3(b). This clause is related to framed structures. We have seen a framed building in the presentation given at the beginning of chapter 9 on 'Flanged sections'. Such framed structures are assumed to consist of two dimensional frames arranged in two mutually perpendicular directions. A two dimensional frame can be seen in the slide no.7 of the presentation. These frames are acted upon by the Live loads and Dead loads which generally act in a 'vertical direction'. The frames are analysed for these loads, and the effects such as Bending moments, Shear forces, Torsions etc., at various points are determined. But some times, Wind and/or Earth quake loads also act on the structure. These loads act in a 'horizontal direction'. So they are called 'lateral loads'. Then the frames of the structure has to be analysed for these lateral loads also. Such frames are called 'lateral load resisting frames'. They have to made much more stronger to resist these additional lateral loads. The fig.15.46 below shows the horizontal forces acting on such a frame.

Fig.15.46

Horizontal forces acting on a frame

If all the loads are 'vertical', the bottom bars will be experiencing zero forces at the supports. But if there is a combination of horizontal loads and vertical loads, stress reversal can occur. In such cases, the bottom bars may experience tensile or compressive forces near the supports. (More details can be obtained from text books on structural analysis of frames.) As the bars experience forces near supports, they have to be given more anchorage. 

We have seen how the anchorage is ensured for bottom bars at simple supports and continuous supports.  We have seen the three parameters related to such simple supports in the previous section:

(i) Length of the embedment. 

(ii) quantity of the bars which are embedded.

(iii) Position of the bars which are embedded.

Here, for lateral load resisting frames, (ii) and (iii) are the same. [(ii) is same as that at a continuous support, which is equal to A_st/4]. 

• But (i) which gives the 'length' is changed from L_d/3 to L_d. That means, we have give the full development length (unique value), and not one third of it. Such an increase will give more anchorage.

We will now see the methods by which this can be achieved at various points in a lateral load resisting frame. The following figs. shows the extensions to be given to the bottom bars when the beam is part of a lateral load resisting frame.

Fig.15.47

Extension into an intermediate Column

From the above fig., we can see that at an intermediate column, there is enough space to extend the bars. So L_d can be easily provided.

Fig.15.48

Extension at an end support with standard 90^o bend

At the end support, we can not extend bars freely. So we may have to provide a bend. The above fig. shows the case when a standard 90^o bend is given. The anchorage value of the portion from B to D is 8Φ. So the total anchorage value is equal to A'B + 8Φ, and this should be greater than or equal to L_d.

Fig.15.49

Extension beyond the bend

Here the anchorage value of the portion from B to D is 8Φ. So the total anchorage value is equal to A'B + 8Φ + DE, and this should be greater than or equal to L_d.

It must be noted that for seismic design of structures, more detailed rules have to be followed by referring the related codes.

Next clause is 26.2.3.3 (c). We have already discussed about it in detail here.

---

So we have seen most of the details about the bottom bars. In the discussions, we saw the extension that has to be given at the supports for the 'continuing bars'. We also saw the extension that has to be given to the 'curtailed bars'. (15.4). Thus we are now in a position to design the curtailment and give the necessary extensions for the bottom bars of various members. After determining the layout and position of the bottom bars using the principles that we saw so far, the check for 'development length' has to be done. The following fig.15.50 can be used to perform this check for the bottom bars in general.

Fig.15.50

Check for development length

There are two types of bars to be considered: 

• Those which are curtailed at some point. The top layer bars in the above fig. is an example for this. They are curtailed at section XX.

• Those which are not curtailed at any point. They continue uninterrupted into the supports. The bottom layer bars in the above fig. is an example of this.

Let XX be the section at which the curtailment is actually done. That is., XX is the section which is determined by making the necessary modifications to the theoretical cut-off point. We know that all the bars (both curtailed and continuing) at the section CL will be under maximum tensile stress. To keep the curtailed bars from 'contracting', the length available is the distance between CL and XX. So this distance must be greater than or equal to L_d (unique value). This length should be available for each of the curtailed bars.

Similarly, at the section XX, the continuing bars will be under maximum tensile stress. So to keep them from 'contracting', each of these bars should have a length which is greater than or equal to L_d . This length should be available on the left side. It may be noted that for the continuing bars, the check for L_d need to be made from the theoretical cut-off section only, and so a greater length is available to qualify as L_d, than if checked from XX.

In the above fig., the mid span section CL is shown, and also the section XX at which curtailment is done is also shown. XX is to the left of CL. So the fig. is a part elevation of the 'left side of a span'. 

As the bars try to contract from both ends, we must provide the necessary L_d  on both sides of the sections being considered. In the above fig., we can see that the bottom bars have a greater distance on the right side of the theoretical cut-off section, as this section is near the left support. But after fixing up the layout of all the bars, we must check and confirm that the required L_d is actually available on both sides of all important sections.

   

If the bars satisfies this check also, the layout and positions of the bottom bars can be finalised.

---

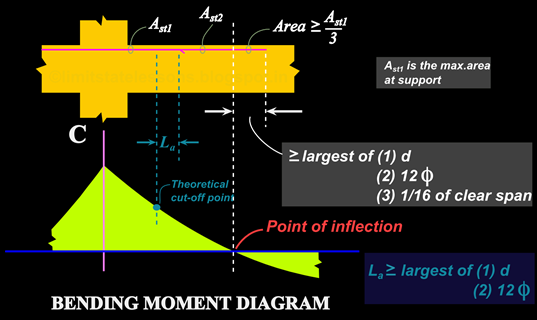
Now we will see the details about the top bars which resist the hogging moment. The requirements regarding these are given in the cl.26.2.3.4 of the code. In this clause, there are two parameters that we have to satisfy. (i) length and (ii) quantity. We will now see the details about each of them:

(i) Length: We know that, after the point of inflection, the moment change from hogging to sagging. So top bars are not required beyond the point of inflection. But the code does not allow us to stop the top bars exactly at that point. It requires us to extend the top bars beyond the point of inflection, to a distance which is greater than the largest of the following:

(1) effective depth d

(2) 12 times the diameter of bar ie., 12Φ

(3) 1⁄16  of clear span.

(ii) Quantity: The continuing bars that goes beyond the point of inflection should have a total area of  A_st ⁄ 3 . where A_st is the maximum area of the top steel at the support.

These two requirements can be discussed in detail with the help of the fig.15.51 below:

Fig.15.51

Curtailment of Top bars

Near the support, an area A_st1 of steel is provided for the top bars in the above fig. Out of these, some bars are curtailed. We can see that the curtailed bars are extended beyond the theoretical point of curtailment, for a distance of L_a. This is based on 15.4 which we derived earlier. But the present clause that we are discussing, is about the continuing bars. The code does not allow us to stop the continuing bars at the point of inflection. But instead, they are extended even beyond the point of inflection by a distance which is greater than or equal to the largest of

(1) effective depth d

(2) 12 times the diameter of bar ie., 12Φ

(3) 1⁄16  of clear span

It can also be seen than the area of these continuing bars is shown to be greater than or equal to A_st1 ⁄ 3.

If we are using a moment envelope, p₀^h should be used as the point of inflection. All the other procedures remain the same. This is shown in the fig.15.52 below:

Fig.15.52

Moment envelope for curtailment of top bars

The arrangements shown in the above can be used also for the framed structures. So these figs. can be used for framed structures just by changing the support from ‘masonry type’ to ‘concrete column’. A 'continuing column' can also be shown if the beam belongs to an intermediate floor. For the top most floor, there will not be a continuing column. All the other details remain the same as in the above figs. The modified figs. for framed structure are shown below:

Fig.15.53
Curtailment of top bars (intermediate support in framed structure)

Fig.15.54

Moment envelope for curtailment of top bars (intermediate support in framed structure)

Now, the above two figs.15.53 and 54 can be used to show the curtailment of top bars at the 'end support of a frame'. For this we have to make some modifications only at the support. The other details remain the same. This is shown in the figs. below:

Fig.15.55

Curtailment of top bars (end support in framed structure)

Fig.15.56

Moment envelope for curtailment of top bars (end support in framed structure)

From the above two figs., we can see that the bars have to be given a standard 90^o bend and should be extended into the column, for obtaining the necessary development length. The anchorage obtained for each bar is equal to A’B + 8Φ + DE. And this anchorage must be greater than or equal to L_d. All other details about the curtailment of bars are the same as that at an intermediate support.

One more detail that we have to see about top bars is when they are provided at a simple support. We will discuss about it in the next section.

PREVIOUS       CONTENTS       NEXT                                          

Copyright©2016 limitstatelessons.blogspot.com- All Rights Reserved

Chapter 15.8 - Development length requirements at inflection points

In the previous section we saw the development length required (at the support) for the bottom bars of a simply supported beam. Now we will see the bottom bars of a continuous beam. Fig.15.38 below is a part elevation showing an intermediate span CD of a continuous beam.

Fig.15.38

Intermediate span of a continuous beam

The fig. also shows the bending moment diagram. The points of inflection are marked as R and S. [The bending moment at the 'points of inflection' is equal to zero. So the portion between the R and S is similar to the portion between the supports of a simply supported beam] The bottom bars provided for the sagging moment between R and S will be under tension, and so will be stretched. They will be trying to contract to their original length. So we can say that, the ends of the bars will be trying to pull inwards (towards the center of the span) from R and S. 

• In the case of simply supported beams, we calculated the minimum length that is available to prevent the pull out from the support.

• In the above continuous beam, our aim is to calculate the minimum length that is available to prevent the contraction of the bottom bars between R and S. Or in other words, the 'pulling out' from R and S.

So both cases are similar. Just as we did in the case of a simply supported beam, here also we can take a small segment pq of the beam for analysis. This small segment is at a distance of l_x from the point of inflection R as shown in the fig.15.39 below:

Fig.15.39

Small segment pq of the beam

The forces on the segment pq will be exactly similar to what we saw in fig.15.30 for the simply supported beam. So the calculations will also be the same, and the available length which will resist the pull out will be derived as M_uR ⁄ V_u. 

• In the case of simply supported beam, V_u is the maximum shear force that occur between the supports. This maximum occurs at the supports.

• In the case of the above continuous beam, V_u is the maximum shear force that occurs between R and S. From the topic on 'Analysis of continuous beams', we know that this maximum occurs exactly at R or S as shown in fig.13.40 below:

Fig.15.40

Shear force diagram

Values immediately to the left of R and to the right of S in the above shear force diagram are higher. But those values are related to the hogging moment at supports. They are not related to the bottom bars. So we can ignore those higher values.

Thus the length M_uR ⁄ V_u  is a part of 'that length of the bar which is within R and S'. This is the least available length that will help to prevent the pull out. 

But the length L₀ if any, beyond R and S will also contribute to prevent the pull out. So, just as the simply supported beam, the total length available to resist the pull out is equal to M_uR ⁄ V_u, + L₀ . It must be greater than or equal to L_d (unique value). So we can write:

L_d (unique value) ≤ M_uR ⁄ V_u + L₀
This expression is same as 15.6 that we derived earlier for simply supported beams.

[It may be noted that, in the fig.15.38 above, the BM diagram shown is that for a uniform loading. There is continuity between sagging and hogging parts. But if Live loads are present, we must consider the ‘envelope’. This topic was discussed in a previous section of this chapter, with the help of fig.15.17. In such a case, the points of inflection to be taken are those marked as  p₀^s in fig.15.17] 

But this L₀ in the case of a point of inflection has an important difference from that in a simply supported beam. According to cl.26.2.3.3 (c) of the code, L₀ at a point of inflection cannot exceed the larger of the following:

(i) d

(ii) 12Φ

This requirement can be detailed as follows:
At an intermediate support, there is enough space to extend the bottom bars to a longer distance. But only a certain length (which is the larger of d or 12Φ) measured from the point of inflection will be eligible to be considered as L₀. This is shown in fig.15.41 below:

Fig.15.41

Restriction on L₀ at point of inflection

In a simply supported beam, there is no such restrictions. The bar can be extended to any distance. We can also give bends (fig.15.36) and even extension beyond bends (fig.15.37). But such measures to increase L₀ should satisfy cover requirements. So it may not be possible to extend the bars to the required length. So in effect, there are restrictions on the availability of L₀ in the cases of both simply supported beams and continuous beams.

We have to satisfy the relation:

L_d (unique value) ≤ M_uR ⁄ V_u + L₀ 

To increase the right side, we can increase L₀ . But we have seen that L₀ has upper limits. Even with the upper limiting value, it may not be possible to satisfy the relation. In such a situation, we can increase M_uR. For this, we will have to reduce the curtailments done to the bottom bars so that more bars reach the support. This method is effective even though it will result in increased costs.

The best solution that the code recommends is to decrease the left side. ie., decrease L_d . Let us see how this can be done:

We have seen the details about L_d , the unique value of development length for a bar of a particular diameter. We have:

In this equation, the diameter Φ is in the numerator. So when Φ increases, L_d also increases and vice versa. This means that, for a larger diameter bar, more length will be required to exert the necessary gripping force to keep it in position with out causing a pull out. And for a bar of lesser diameter, lesser length will be sufficient. 

We have:
L_d (unique value) ≤ M_uR ⁄ V_u + L₀
Thus by using bars of lower diameter, the left side of the above expression can be reduced. By reducing the left side, we have a better chance of satisfying the condition. Thus, if even after providing the maximum allowable value of L₀, the condition cannot be satisfied, we must reduce the diameter of the bars and check again. However, we must remember that we cannot use very low diameter bars. Diameters less than 12 mm are not generally used for bottom bars of beams.

So now we know how to ensure that 'the development length requirements are satisfied at the simple supports and at the points of inflection'. The required length should be provided for all the bars at the support or at the inflection point.

In the next section, we will discuss about the code requirements regarding the curtailment of bars.

PREVIOUS       CONTENTS       NEXT                                          

Copyright©2016 limitstatelessons.blogspot.com - All Rights Reserved

Chapter 15.2 - Curtailment at points of inflection

In the previous section we saw the method of finding the theoretical point of curtailment at more than one section along the length of the beam. In this section we will see the method for the top bars which resist the hogging moment at an intermediate support of a continuous beam.

In fact the method is the same: Find the M_uR obtained from the remaining bars, and put it in the equation to obtain 'x'. So we will discuss only the general scheme adopted for the top bars. This is shown in the fig.15.9 below:

Fig.15.11
Curtailment of top bars

• The first curtailment is given to the bars in the bottom most layer (when counted from the top) among the top bars. When they are curtailed, the steel that remains is A_st2. 
• The second curtailment is given to the second bottom most layer. After this curtailment, the steel that remains is A_st3. 

When we follow this pattern, greater quantities of steel are available at the regions nearer to the support. This indeed must be the case because, stresses are greater near the supports as far as the 'top bars for hogging moments' are concerned.

Another aspect to note is the position of 'points of inflection'. These are the points where the bending moment changes sign. The hogging nature of the bending moment at the support continues upto the points of inflection. So we have to provide top steel upto the point of inflection. Similarly, the sagging nature of the bending moment at the midspan region also continues upto the points of inflection. So we have to provide the bottom steel upto these points. But we can follow the principles of curtailment, and progressively reduce the quantity of steel at the sections near the points of inflection.

We will now discuss another aspect of the point of inflection. In continuous beams, the maximum bending moment at any section will depend upon the position of the loads along the spans. The DL will be present at all times, and it's position will not change. But the LL will change position. In order to find the maximum bending moment at a section, we have to place the LL in those positions that give maximum bending moment at that section, and then analyse the whole continuous beam. This topic is dealt with in 'influence lines' in Structural analysis classes. 

We had a basic discussion about it in the second section of chapter 7, 'Analysis of a continuous beam'. Let us consider the solved example of a continuous beam ABCDE given in that chapter. We do not require the bending moments or final results obtained in that example. We are interested only in the pattern of loading that we adopted for that beam. This pattern was shown in fig.7.19 and 7.20. 

Let us consider the support C, and the span CD. We want 
• the maximum hogging moment at support C and 
• the maximum sagging moment in the span CD. 
For obtaining the maximum possible hogging moment at support C, we must place the LL on the adjacent spans BC and CD, and also on alternate spans. But after filling up BC and CD, there are no alternate spans. So we will filled up BC and CD with LL, and then analysed the whole beam. The resulting BM diagram is shown below in fig.15.12:

Fig.15.12
Maximum hogging moment at support C

But this BM diagram is prepared xxx exclusively for the hogging moment at support C. That is., only the hogging moment values at the support C should be obtained from this diagram. So we will remove the unwanted parts to obtain the fig.15.13 shown below:

Fig.15.13
Diagram with unwanted values removed

Now we will look at the span CD. For maximum sagging moment in this span, the LL should be placed on CD and on alternate spans. So we placed it on CD and on the first span AB. The resulting BM diagram is shown in the fig.15.14 below:

Fig.15.14
Maximum sagging moment in span CD

But this BM diagram is prepared exclusively for the sagging moment in span CD. That is., only the sagging moment values in span CD should be obtained from this diagram. [For this particular beam ABCDE, the above loading arrangement for the maximum sagging moment in CD is same as the loading arrangement for the maximum sagging moment in AB also. But we are not considering AB in our present discussion]. So we will remove the unwanted parts to obtain the fig.15.13 shown below:

Fig.15.15
Diagram with unwanted values removed

The figs.15.15 and 15.13 gives the required values. So we can combine the two figs. as shown below:

Fig.15.16
Required values shown in a single diagram.

The above fig.15.16 gives the maximum values of the hogging moment at support C and the sagging moment in span CD. By using the same procedure, we can fill up the remaining supports and spans in the fig. Then, from that single fig., we can obtain the maximum values at any section along the length of ABCDE. Such a fig. is called the 'moment envelope'. Now let us take a closer look at the fig.15.14. This is shown in the fig.15.17 below:

Fig.15.17
Details of the moment envelope at support C and span CD and the points of inflection

We can see that the point of zero moment in the hogging moment envelope which is marked as p₀^h is different from p₀^s the point of zero moment in the sagging moment envelope. This is a situation that we often see while analysing continuous beams and continuous one-way slabs.

• The top steel bars should be provided for the hogging moment in the region shown in orange colour in the above fig.15.17. This steel should be available upto the points where the orange graph meets the horizontal axis, which are the points of inflection. In fact, as we will soon see in later sections, the bars should be continued even beyond the points of inflection.

• The bottom steel bars should be provided for the sagging moment in the region shown in yellow colour in the above fig.15.17. This steel should be available upto the points where the yellow graph meets the horizontal axis, which are the points of inflection. In this case also, we will soon see in later sections that, the bars should be continued even beyond the points of inflection.

• So the points of inflection play a major role in the final layout of bars. But these points of inflection for the sagging and hogging moments may not coincide. That is., we cannot expect a 'continuity' at the points of inflection as we saw in the fig.15.11 earlier in this section. The meeting point with the horizontal axis may be different for sagging and hogging moments, just as p₀^h and p₀^s in the fig.15.17. This happens when the different positions of LL are considered. This non-coincidence should be considered, and exact positions of various points of inflection should be determined (from the moment envelope) so as to provide a satisfactory lay out of bars.

In the next section, we will discuss another method to determine the theoretical cut-off points.

PREVIOUS       CONTENTS       NEXT                                          

Copyright©2016 limitstatelessons.blogspot.com - All Rights Reserved