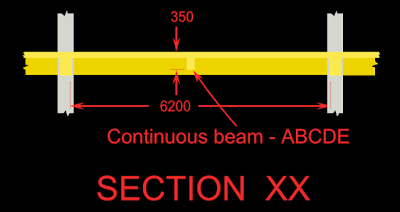
In this section we will calculate the effective spans of the continuous slab shown in the fig.7e.1 below:
Fig.7e.1
Plan and elevation of continuous slab
From the fig., we can see that, in this problem, the supports have different widths. The outer two walls on either sides have a width of 200mm and the middle wall have a width of 230mm.
We will calculate the effective spans by the two different methods: The one based on Eurocode-2, and the other based on IS 456. For this problem, it is convenient to mention before hand that, each of the spans have their support widths less than it's ln/12. So while using the cl.22.2(b) of IS 456, we will not have to look to the portion below the magenta colored dashed line of the chart. (Fig.7a.4)
Also assume dia. of bottom bars = 10 mm and Cc = 30 mm
So effective depth d = 150 -30 -5 = 115 mm
First we will consider span AB. The calculations based on Eurocode-2 is shown in Table 7e.1 below:
Table 7e.1
Span AB, ln =2850
Clear span ln =2850mm.
ln/12 = 2850/12 =237.50. So t1 < ln/12 & t2 < ln/12
As mentioned above, we only need the portion above the magenta colored dashed line for all spans of the beam. This is shown in the fig.7e.2 below. This fig. is applicable to all the spans.
Fig.7e.2
Application of chart to span AB
Now we calculate the following:
• c/c distance between the supports = 2850 +100 +100 =3050
• clear span + effective depth = 2850 +115 =2965
Effective span = leff = Lesser of the above = 2965mm
Thus we calculated leff of span AB using the two methods.
Now we will consider span BC. The calculations based on Eurocode-2 is shown in Table 7e.2 below:
Table 7e.2
Span BC, ln =3300
Clear span ln =3300mm.
ln/12 = 3300/12 =275.00. So t1 < ln/12 & t2 < ln/12
Fig.7b.2 is applicable here also. Now we calculate the following:
• c/c distance between the supports = 3300 +100 +115 =3515
• clear span + effective depth = 3300 +115 =3415
Effective span = leff = Lesser of the above = 3415mm
Thus we calculated leff of span BC using the two methods.
Now we will consider span CD. The calculations based on Eurocode-2 is shown in Table 7e.3 below:
Table 7e.3
Span CD, ln =3300
Clear span ln =3300mm.
ln/12 = 3300/12 =275.00. So t1 < ln/12 & t2 < ln/12
Fig.7e.2 is applicable here also. Now we calculate the following:
• c/c distance between the supports = 3300 +115 +100 =3515
• clear span + effective depth = 3300 +115 =3415
Effective span = leff = Lesser of the above = 3415mm
Thus we calculated leff of span CD using the two methods.
Now we will consider span DE. The calculations based on Eurocode-2 is shown in Table 7e.4 below:
Table 7e.4
Span DE, ln =2850
Clear span ln =2850mm.
ln/12 = 2850/12 =237.50. So t1 < ln/12 & t2 < ln/12
Fig.7e.2 is applicable here also. Now we calculate the following:
• c/c distance between the supports = 2850 +100 +100 =3050
• clear span + effective depth = 2850 +115 =2965
Effective span = leff = Lesser of the above = 2965mm
Thus we calculated leff of span DE using the two methods. All the results from the two methods are tabulated below:
We have branched off from the main discussion. The layout map given below will help us to navigate easily between the various sections. Links to some more examples are also given in the layout map.
Fig.7e.1
Plan and elevation of continuous slab
From the fig., we can see that, in this problem, the supports have different widths. The outer two walls on either sides have a width of 200mm and the middle wall have a width of 230mm.
We will calculate the effective spans by the two different methods: The one based on Eurocode-2, and the other based on IS 456. For this problem, it is convenient to mention before hand that, each of the spans have their support widths less than it's ln/12. So while using the cl.22.2(b) of IS 456, we will not have to look to the portion below the magenta colored dashed line of the chart. (Fig.7a.4)
Also assume dia. of bottom bars = 10 mm and Cc = 30 mm
So effective depth d = 150 -30 -5 = 115 mm
First we will consider span AB. The calculations based on Eurocode-2 is shown in Table 7e.1 below:
Table 7e.1
Span AB, ln =2850
| Support A | Support B | |
| Type of support | Non-continuous support | Continuous support |
| Fig. to use | Fig.(a) | Fig.(b) |
| h | 150 | 150 |
| t | 200 | 200 |
| ai = lesser of {h/2; t/2} | 75 | 75 |
leff = ln + a1 +a2 =2850 +75 +75 =3000
The calculations based on IS 456 is given below:Clear span ln =2850mm.
ln/12 = 2850/12 =237.50. So t1 < ln/12 & t2 < ln/12
As mentioned above, we only need the portion above the magenta colored dashed line for all spans of the beam. This is shown in the fig.7e.2 below. This fig. is applicable to all the spans.
Fig.7e.2
Application of chart to span AB
Now we calculate the following:
• c/c distance between the supports = 2850 +100 +100 =3050
• clear span + effective depth = 2850 +115 =2965
Effective span = leff = Lesser of the above = 2965mm
Thus we calculated leff of span AB using the two methods.
Now we will consider span BC. The calculations based on Eurocode-2 is shown in Table 7e.2 below:
Table 7e.2
Span BC, ln =3300
| Support B | Support C | |
| Type of support | Continuous support | Continuous support |
| Fig. to use | Fig.(b) | Fig.(b) |
| h | 150 | 150 |
| t | 200 | 230 |
| ai = lesser of {h/2; t/2} | 75 | 75 |
leff = ln + a1 +a2 =3300 +75 +75 =3450
The calculations based on IS 456 is given below:Clear span ln =3300mm.
ln/12 = 3300/12 =275.00. So t1 < ln/12 & t2 < ln/12
Fig.7b.2 is applicable here also. Now we calculate the following:
• c/c distance between the supports = 3300 +100 +115 =3515
• clear span + effective depth = 3300 +115 =3415
Effective span = leff = Lesser of the above = 3415mm
Thus we calculated leff of span BC using the two methods.
Now we will consider span CD. The calculations based on Eurocode-2 is shown in Table 7e.3 below:
Table 7e.3
Span CD, ln =3300
| Support C | Support D | |
| Type of support | Continuous support | Continuous support |
| Fig. to use | Fig.(b) | Fig.(b) |
| h | 150 | 150 |
| t | 230 | 200 |
| ai = lesser of {h/2; t/2} | 75 | 75 |
leff = ln + a1 +a2 =3300 +75 +75 =3450
The calculations based on IS 456 is given below:Clear span ln =3300mm.
ln/12 = 3300/12 =275.00. So t1 < ln/12 & t2 < ln/12
Fig.7e.2 is applicable here also. Now we calculate the following:
• c/c distance between the supports = 3300 +115 +100 =3515
• clear span + effective depth = 3300 +115 =3415
Effective span = leff = Lesser of the above = 3415mm
Thus we calculated leff of span CD using the two methods.
Now we will consider span DE. The calculations based on Eurocode-2 is shown in Table 7e.4 below:
Table 7e.4
Span DE, ln =2850
| Support D | Support E | |
| Type of support | Continuous support | Non-Continuous support |
| Fig. to use | Fig.(b) | Fig.(a) |
| h | 150 | 150 |
| t | 200 | 200 |
| ai = lesser of {h/2; t/2} | 75 | 75 |
leff = ln + a1 +a2 =2850 +75 +75 =3000
The calculations based on IS 456 is given below:Clear span ln =2850mm.
ln/12 = 2850/12 =237.50. So t1 < ln/12 & t2 < ln/12
Fig.7e.2 is applicable here also. Now we calculate the following:
• c/c distance between the supports = 2850 +100 +100 =3050
• clear span + effective depth = 2850 +115 =2965
Effective span = leff = Lesser of the above = 2965mm
Thus we calculated leff of span DE using the two methods. All the results from the two methods are tabulated below:
Table 7e.5: Effective spans
| Name of span | Based on Euro code | Based on IS456 |
| AB | 3000 | 2965 |
| BC | 3450 | 3415 |
| CD | 3450 | 3415 |
| DE | 3000 | 2965 |
We have branched off from the main discussion. The layout map given below will help us to navigate easily between the various sections. Links to some more examples are also given in the layout map.
Copyright©2015 limitstatelessons.blogspot.in - All Rights Reserved