To analyse a continuous beam or slab, we must know the 'effective span' of each of the spans of the beam or slab. Various codes gives different methods to calculate the effective span. First we will see the provisions in Eurocode-2. Then we will discuss the provisions in IS 456.
In the cl 5.3.2.2 of the Eurocode-2, the basic formula for finding the effective span is given as
Eq.7a.1: leff = ln + a1 + a2
where:
ln is the clear distance between the faces of the supports,
a1 and a2 are the quantities at the beginning and end of a member which are to be determined from the appropriate ai values in fig 5.4 of EC-2. This fig. is shown in Fig.7a.1 below:
Fig.7a.1
Effective span calculation
We will now do an example which will demonstrate the application of the above fig.7a.1. While doing example, we will also check the provisions given by IS 456.
Example 1:
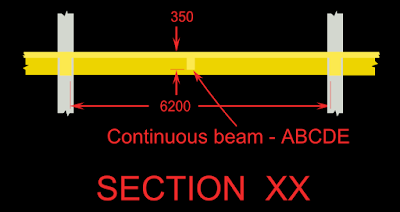
The continuous beam ABCDE is part of a framed structure. It is a secondary beam, supported on some primary beams. The width of each of these primary beams is 300 mm. The clear spans and other details are shown in the fig.7a.2 below:
Fig.7a.2
Part plan
Calculations:
Let us first take span AB. Clear span ln =3850mm
• Support 'A' is non-continuous.
• So we have to use (a) of Fig.7a.1 above.
• Height of the beam is 350mm. So h = 350
• Width of the supporting beam is 300mm. So t =300
• Value of ai is the lesser of h/2 and t/2. So a1 =lesser of {350/2 ; 300/2} = 150
• Support 'B' is continuous.
• So we have to use (b) of Fig.7a.1 above.
• Height of the beam is 350mm. So h = 350
• Width of the supporting beam is 300mm. So t =300
• Value of ai is the lesser of h/2 and t/2. So a2 =lesser of {350/2 ; 300/2} = 150
From Eq.7a.1, leff = ln + a1 + a2 =3850 +150 +150 =4150mm
The above result can be summarized as in Table 7a.1 below:
Fig.7a.3
Effective span using IS456
From the above 'flow chart', we can see that the first branching takes place depending on the width of the support. If the widths are less than 1/12 of the clear span, then the effective span can be calculated by the same method that we would use for a simply supported span. If the width of the support is not less than 1/12 of the clear span, we have to do more calculations:
The next branching takes place depending on whether the span that we are considering is an end span, or an intermediate span.
If it is an end span, further branching takes place depending on whether one end is 'fixed' or 'free'.
We will now apply the above chart to the span AB of our example.
Clear span ln =3850mm.
Here we have to consider both the supports at the same time. So we will denote their widths as t1 and t2.
t1 =300; t2 =300
ln/12 = 3850/12 =320.83. So t1 < ln/12 & t2 < ln/12
Thus we branch towards the left in the flow chart. This is shown in the fig.7a.4 below. The path taken through the chart is indicated by the yellow colored arrow line. The point of branching is indicated as 'A'.
Fig.7a.4
Application of the chart to span AB
Once we find that the widths are less than 1/12 of the clear span, the result is obvious: use cl.22.2(a). So the portion below the dashed magenta colored line is not applicable to our span AB.
Thus our next aim is to apply cl.22.2(a). We have used this clause previously for simply supported slabs and beams. The details about this clause can be seen here. We have to calculate the effective depth of the beam. For this we have to assume the diameter of the main bars and also the diameter of the links. If we assume 20mm and 8 mm respectively, we will get the effective cover as 48mm for 'moderate' exposure condition. (effective cover = 30 +8 +10 =48). So the effective depth d for our beam = 350 -48 =302mm.
Now we calculate the following:
• c/c distance between the supports = 3850 +300 =4150
• clear span + effective depth = 3850 +302 =4152
Effective span = leff = Lesser of the above = 4150mm
Thus we calculated leff of span AB using two methods.
Now we will consider span BC. The calculations based on Eurocode-2 is shown in Table 7a.2 below:
Table 7a.2
Span BC, ln =4200
Clear span ln =4200mm.
ln/12 = 4200/12 =350. So t1 < ln/12 & t2 < ln/12
So we branch to the left at point 'A', just as we did in the case of span AB. This is shown in the fig.7a.5 below:
Fig.7a.5
Application of chart to span BC
The portion of the chart which lies below the magenta colored dashed line is not applicable to span BC.
Now we calculate the following:
• c/c distance between the supports = 4200 +300 =4500
• clear span + effective depth = 4200 +302 =4502
Effective span = leff = Lesser of the above = 4500mm
Thus we calculated leff of span BC using two methods.
Now we will consider span CD. The calculations based on Eurocode-2 is shown in Table 7a.3 below:
Table 7a.3
Span CD, ln =3950
Clear span ln =3950mm.
ln/12 = 3950/12 =329.17. So t1 < ln/12 & t2 < ln/12
So we branch to the left at point 'A', just as we did in the case of spans AB and BC. We can use the same fig.7a.5 above.
The portion of the chart which lies below the magenta colored dashed line is not applicable to span CD also.
Now we calculate the following:
• c/c distance between the supports = 3950 +300 =4250
• clear span + effective depth = 3950 +302 =4252
Effective span = leff = Lesser of the above = 4250mm
Thus we calculated leff of span CD using two methods.
Now we will consider span DE. The calculations based on Eurocode-2 is shown in Table 7a.4 below:
Table 7a.4
Span DE, ln =3950
Clear span ln =3950mm.
ln/12 = 3950/12 =329.17. So t1 < ln/12 & t2 < ln/12
So we branch to the left at point 'A', just as we did in the case of spans AB and BC. We can use the same fig.7a.5 above.
The portion of the chart which lies below the magenta colored dashed line is not applicable to span DE also.
Now we calculate the following:
• c/c distance between the supports = 3950 +300 =4250
• clear span + effective depth = 3950 +302 =4252
Effective span = leff = Lesser of the above = 4250mm
Thus we calculated leff of span DE using two methods. All the results from the two methods are tabulated below:
Thus we have seen two methods for calculating the effective span.
We have branched off from the main discussion. The layout map given below will help us to navigate easily between the various sections. Links to some more examples are also given in the layout map.
In the cl 5.3.2.2 of the Eurocode-2, the basic formula for finding the effective span is given as
Eq.7a.1: leff = ln + a1 + a2
where:
ln is the clear distance between the faces of the supports,
a1 and a2 are the quantities at the beginning and end of a member which are to be determined from the appropriate ai values in fig 5.4 of EC-2. This fig. is shown in Fig.7a.1 below:
Fig.7a.1
Effective span calculation
We will now do an example which will demonstrate the application of the above fig.7a.1. While doing example, we will also check the provisions given by IS 456.
Example 1:
The continuous beam ABCDE is part of a framed structure. It is a secondary beam, supported on some primary beams. The width of each of these primary beams is 300 mm. The clear spans and other details are shown in the fig.7a.2 below:
Fig.7a.2
Part plan
Calculations:
Let us first take span AB. Clear span ln =3850mm
• Support 'A' is non-continuous.
• So we have to use (a) of Fig.7a.1 above.
• Height of the beam is 350mm. So h = 350
• Width of the supporting beam is 300mm. So t =300
• Value of ai is the lesser of h/2 and t/2. So a1 =lesser of {350/2 ; 300/2} = 150
• Support 'B' is continuous.
• So we have to use (b) of Fig.7a.1 above.
• Height of the beam is 350mm. So h = 350
• Width of the supporting beam is 300mm. So t =300
• Value of ai is the lesser of h/2 and t/2. So a2 =lesser of {350/2 ; 300/2} = 150
From Eq.7a.1, leff = ln + a1 + a2 =3850 +150 +150 =4150mm
The above result can be summarized as in Table 7a.1 below:
Table 7a.1
Span AB, ln =3850
Span AB, ln =3850
| Support A | Support B | |
| Type of support | Non-continuous support | Continuous support |
| Fig. to use | Fig.(a) | Fig.(b) |
| h | 350 | 350 |
| t | 300 | 300 |
| ai = lesser of {h/2; t/2} | 150 | 150 |
leff = ln + a1
+a2 =4150
Now let us calculate the effective span of this same span using the provisions given in IS456. The clause applicable to continuous beams and slabs is cl.22.2(b). A 'flow chart' like presentation of this clause is given below:Fig.7a.3
Effective span using IS456
From the above 'flow chart', we can see that the first branching takes place depending on the width of the support. If the widths are less than 1/12 of the clear span, then the effective span can be calculated by the same method that we would use for a simply supported span. If the width of the support is not less than 1/12 of the clear span, we have to do more calculations:
The next branching takes place depending on whether the span that we are considering is an end span, or an intermediate span.
If it is an end span, further branching takes place depending on whether one end is 'fixed' or 'free'.
We will now apply the above chart to the span AB of our example.
Clear span ln =3850mm.
Here we have to consider both the supports at the same time. So we will denote their widths as t1 and t2.
t1 =300; t2 =300
ln/12 = 3850/12 =320.83. So t1 < ln/12 & t2 < ln/12
Thus we branch towards the left in the flow chart. This is shown in the fig.7a.4 below. The path taken through the chart is indicated by the yellow colored arrow line. The point of branching is indicated as 'A'.
Fig.7a.4
Application of the chart to span AB
Once we find that the widths are less than 1/12 of the clear span, the result is obvious: use cl.22.2(a). So the portion below the dashed magenta colored line is not applicable to our span AB.
Thus our next aim is to apply cl.22.2(a). We have used this clause previously for simply supported slabs and beams. The details about this clause can be seen here. We have to calculate the effective depth of the beam. For this we have to assume the diameter of the main bars and also the diameter of the links. If we assume 20mm and 8 mm respectively, we will get the effective cover as 48mm for 'moderate' exposure condition. (effective cover = 30 +8 +10 =48). So the effective depth d for our beam = 350 -48 =302mm.
Now we calculate the following:
• c/c distance between the supports = 3850 +300 =4150
• clear span + effective depth = 3850 +302 =4152
Effective span = leff = Lesser of the above = 4150mm
Thus we calculated leff of span AB using two methods.
Now we will consider span BC. The calculations based on Eurocode-2 is shown in Table 7a.2 below:
Table 7a.2
Span BC, ln =4200
| Support B | Support C | |
| Type of support | Continuous support | Continuous support |
| Fig. to use | Fig.(b) | Fig.(b) |
| h | 350 | 350 |
| t | 300 | 300 |
| ai = lesser of {h/2; t/2} | 150 | 150 |
leff = ln + a1 +a2 =4200 +150 +150 =4500
The calculations based on IS 456 is given below:Clear span ln =4200mm.
ln/12 = 4200/12 =350. So t1 < ln/12 & t2 < ln/12
So we branch to the left at point 'A', just as we did in the case of span AB. This is shown in the fig.7a.5 below:
Fig.7a.5
Application of chart to span BC
The portion of the chart which lies below the magenta colored dashed line is not applicable to span BC.
Now we calculate the following:
• c/c distance between the supports = 4200 +300 =4500
• clear span + effective depth = 4200 +302 =4502
Effective span = leff = Lesser of the above = 4500mm
Thus we calculated leff of span BC using two methods.
Now we will consider span CD. The calculations based on Eurocode-2 is shown in Table 7a.3 below:
Table 7a.3
Span CD, ln =3950
| Support C | Support D | |
| Type of support | Continuous support | Continuous support |
| Fig. to use | Fig.(b) | Fig.(b) |
| h | 350 | 350 |
| t | 300 | 300 |
| ai = lesser of {h/2; t/2} | 150 | 150 |
leff = ln + a1 +a2 =3950 +150 +150 =4250
The calculations based on IS 456 is given below:Clear span ln =3950mm.
ln/12 = 3950/12 =329.17. So t1 < ln/12 & t2 < ln/12
So we branch to the left at point 'A', just as we did in the case of spans AB and BC. We can use the same fig.7a.5 above.
The portion of the chart which lies below the magenta colored dashed line is not applicable to span CD also.
Now we calculate the following:
• c/c distance between the supports = 3950 +300 =4250
• clear span + effective depth = 3950 +302 =4252
Effective span = leff = Lesser of the above = 4250mm
Thus we calculated leff of span CD using two methods.
Now we will consider span DE. The calculations based on Eurocode-2 is shown in Table 7a.4 below:
Table 7a.4
Span DE, ln =3950
| Support D | Support E | |
| Type of support | Continuous support | Non-continuous support |
| Fig. to use | Fig.(b) | Fig.(a) |
| h | 350 | 350 |
| t | 300 | 300 |
| ai = lesser of {h/2; t/2} | 150 | 150 |
leff = ln + a1 +a2 =3950 +150 +150 =4250
The calculations based on IS 456 is given below:Clear span ln =3950mm.
ln/12 = 3950/12 =329.17. So t1 < ln/12 & t2 < ln/12
So we branch to the left at point 'A', just as we did in the case of spans AB and BC. We can use the same fig.7a.5 above.
The portion of the chart which lies below the magenta colored dashed line is not applicable to span DE also.
Now we calculate the following:
• c/c distance between the supports = 3950 +300 =4250
• clear span + effective depth = 3950 +302 =4252
Effective span = leff = Lesser of the above = 4250mm
Thus we calculated leff of span DE using two methods. All the results from the two methods are tabulated below:
Table 7a.5: Effective spans
| Name of span | Based on Euro code | Based on IS456 |
| AB | 4150 | 4150 |
| BC | 4500 | 4500 |
| CD | 4250 | 4250 |
| DE | 4250 | 4250 |
Thus we have seen two methods for calculating the effective span.
We have branched off from the main discussion. The layout map given below will help us to navigate easily between the various sections. Links to some more examples are also given in the layout map.
Copyright ©2015 limitstatelessons.blogspot.com - All Rights Reserved






No comments:
Post a Comment