In the previous section we saw the lengths of bars and areas of bars that have to be embedded at a simple support and at a continuous support. These requirements are given in the sub clause (a) of 26.2.3.3.
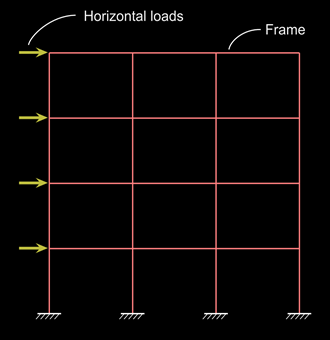
Now we will see the next sub clause: cl.26.2.3.3(b). This clause is related to framed structures. We have seen a framed building in the presentation given at the beginning of chapter 9 on 'Flanged sections'. Such framed structures are assumed to consist of two dimensional frames arranged in two mutually perpendicular directions. A two dimensional frame can be seen in the slide no.7 of the presentation. These frames are acted upon by the Live loads and Dead loads which generally act in a 'vertical direction'. The frames are analysed for these loads, and the effects such as Bending moments, Shear forces, Torsions etc., at various points are determined. But some times, Wind and/or Earth quake loads also act on the structure. These loads act in a 'horizontal direction'. So they are called 'lateral loads'. Then the frames of the structure has to be analysed for these lateral loads also. Such frames are called 'lateral load resisting frames'. They have to made much more stronger to resist these additional lateral loads. The fig.15.46 below shows the horizontal forces acting on such a frame.Fig.15.46
Horizontal forces acting on a frame
If all the loads are 'vertical', the bottom bars will be experiencing zero forces at the supports. But if there is a combination of horizontal loads and vertical loads, stress reversal can occur. In such cases, the bottom bars may experience tensile or compressive forces near the supports. (More details can be obtained from text books on structural analysis of frames.) As the bars experience forces near supports, they have to be given more anchorage.
We have seen how the anchorage is ensured for bottom bars at simple supports and continuous supports. We have seen the three parameters related to such simple supports in the previous section:
(i) Length of the embedment.
(ii) quantity of the bars which are embedded.
(iii) Position of the bars which are embedded.
Here, for lateral load resisting frames, (ii) and (iii) are the same. [(ii) is same as that at a continuous support, which is equal to Ast/4].
We will now see the methods by which this can be achieved at various points in a lateral load resisting frame. The following figs. shows the extensions to be given to the bottom bars when the beam is part of a lateral load resisting frame.
Extension into an intermediate Column
From the above fig., we can see that at an intermediate column, there is enough space to extend the bars. So Ld can be easily provided.
Extension at an end support with standard 90o bend
At the end support, we can not extend bars freely. So we may have to provide a bend. The above fig. shows the case when a standard 90o bend is given. The anchorage value of the portion from B to D is 8Φ. So the total anchorage value is equal to A'B + 8Φ, and this should be greater than or equal to Ld.
Fig.15.49
Extension beyond the bend
Here the anchorage value of the portion from B to D is 8Φ. So the total anchorage value is equal to A'B + 8Φ + DE, and this should be greater than or equal to Ld.
It must be noted that for seismic design of structures, more detailed rules have to be followed by referring the related codes.
Next clause is 26.2.3.3 (c). We have already discussed about it in detail here.
So we have seen most of the details about the bottom bars. In the discussions, we saw the extension that has to be given at the supports for the 'continuing bars'. We also saw the extension that has to be given to the 'curtailed bars'. (15.4). Thus we are now in a position to design the curtailment and give the necessary extensions for the bottom bars of various members. After determining the layout and position of the bottom bars using the principles that we saw so far, the check for 'development length' has to be done. The following fig.15.50 can be used to perform this check for the bottom bars in general.
There are two types of bars to be considered:
• Those which are curtailed at some point. The top layer bars in the above fig. is an example for this. They are curtailed at section XX.
• Those which are not curtailed at any point. They continue uninterrupted into the supports. The bottom layer bars in the above fig. is an example of this.
Let XX be the section at which the curtailment is actually done. That is., XX is the section which is determined by making the necessary modifications to the theoretical cut-off point. We know that all the bars (both curtailed and continuing) at the section CL will be under maximum tensile stress. To keep the curtailed bars from 'contracting', the length available is the distance between CL and XX. So this distance must be greater than or equal to Ld (unique value). This length should be available for each of the curtailed bars.
Similarly, at the section XX, the continuing bars will be under maximum tensile stress. So to keep them from 'contracting', each of these bars should have a length which is greater than or equal to Ld . This length should be available on the left side. It may be noted that for the continuing bars, the check for Ld need to be made from the theoretical cut-off section only, and so a greater length is available to qualify as Ld, than if checked from XX.
In the above fig., the mid span section CL is shown, and also the section XX at which curtailment is done is also shown. XX is to the left of CL. So the fig. is a part elevation of the 'left side of a span'.
As the bars try to contract from both ends, we must provide the necessary Ld on both sides of the sections being considered. In the above fig., we can see that the bottom bars have a greater distance on the right side of the theoretical cut-off section, as this section is near the left support. But after fixing up the layout of all the bars, we must check and confirm that the required Ld is actually available on both sides of all important sections.
If the bars satisfies this check also, the layout and positions of the bottom bars can be finalised.
Now we will see the details about the top bars which resist the hogging moment. The requirements regarding these are given in the cl.26.2.3.4 of the code. In this clause, there are two parameters that we have to satisfy. (i) length and (ii) quantity. We will now see the details about each of them:
(i) Length: We know that, after the point of inflection, the moment change from hogging to sagging. So top bars are not required beyond the point of inflection. But the code does not allow us to stop the top bars exactly at that point. It requires us to extend the top bars beyond the point of inflection, to a distance which is greater than the largest of the following:
(1) effective depth d
(2) 12 times the diameter of bar ie., 12Φ
(3) 1⁄16 of clear span.
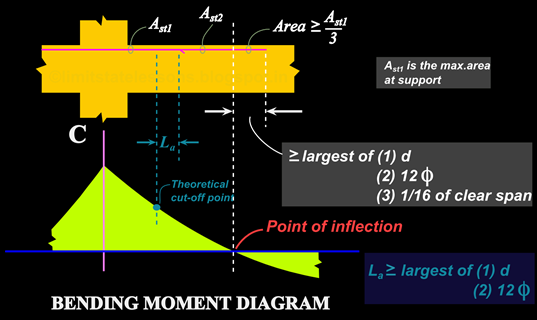
(ii) Quantity: The continuing bars that goes beyond the point of inflection should have a total area of Ast ⁄ 3 . where Ast is the maximum area of the top steel at the support.
These two requirements can be discussed in detail with the help of the fig.15.51 below:
Curtailment of Top bars
Near the support, an area Ast1 of steel is provided for the top bars in the above fig. Out of these, some bars are curtailed. We can see that the curtailed bars are extended beyond the theoretical point of curtailment, for a distance of La. This is based on 15.4 which we derived earlier. But the present clause that we are discussing, is about the continuing bars. The code does not allow us to stop the continuing bars at the point of inflection. But instead, they are extended even beyond the point of inflection by a distance which is greater than or equal to the largest of
(1) effective depth d
(2) 12 times the diameter of bar ie., 12Φ
(3) 1⁄16 of clear span
It can also be seen than the area of these continuing bars is shown to be greater than or equal to Ast1 ⁄ 3.
If we are using a moment envelope, p0h should be used as the point of inflection. All the other procedures remain the same. This is shown in the fig.15.52 below:
Moment envelope for curtailment of top bars
The arrangements shown in the above can be used also for the framed structures. So these figs. can be used for framed structures just by changing the support from ‘masonry type’ to ‘concrete column’. A 'continuing column' can also be shown if the beam belongs to an intermediate floor. For the top most floor, there will not be a continuing column. All the other details remain the same as in the above figs. The modified figs. for framed structure are shown below:
Fig.15.54
Moment envelope for curtailment of top bars (intermediate support in framed structure)
Now, the above two figs.15.53 and 54 can be used to show the curtailment of top bars at the 'end support of a frame'. For this we have to make some modifications only at the support. The other details remain the same. This is shown in the figs. below:
Fig.15.56
Moment envelope for curtailment of top bars (end support in framed structure)
From the above two figs., we can see that the bars have to be given a standard 90o bend and should be extended into the column, for obtaining the necessary development length. The anchorage obtained for each bar is equal to A’B + 8Φ + DE. And this anchorage must be greater than or equal to Ld. All other details about the curtailment of bars are the same as that at an intermediate support.
One more detail that we have to see about top bars is when they are provided at a simple support. We will discuss about it in the next section.
Copyright©2016 limitstatelessons.blogspot.com- All Rights Reserved









No comments:
Post a Comment