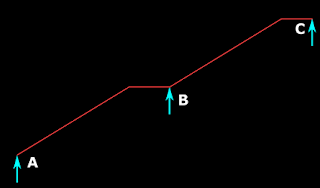
In the previous section we saw the support A of the stair. Now we will see the other supports. End B of flight AB is resting on a masonry wall. This is similar to an ordinary horizontal slab resting on a masonry wall, and is treated as a simple support. In the same way, the end C of flight CD, which is resting on the same wall, is also a simple support.
Now we consider end D. It is resting on a reinforced concrete beam. This beam is a part of the main building. It should have adequate support from the main building. It should also be properly restrained against rotation and/or over turning. Stability of this beam should be ensured while the design and construction of the Main building itself. When the end D of the stair rests on the beam, some extra bars are provided which will properly anchor the stair onto the beam. These bars are provided only to prevent the sliding of the flight CD. They do not resist any bending moment. Considering the above points, The support D is also considered as a Simple support.
So we can modify fig.16.6 by adding the support conditions. This is shown in the fig.16.8 below:
Fig.16.8
Supports of stair flights
So we have fixed up all the supports for the stair.
At this time we will take a quick look at another type of support commonly seen in practice. That is., the 'continuous support'. An example of this is shown in the fig.16.9 below:
Fig.16.9
Example of a continuous support for stairs
ABC is a stair. It consists of two flights AB and BC. But we cannot separate the two flights. The whole stair ABC should be analysed as a single unit. Support B should be treated as a 'continuous support'. A continuous support can come within a single flight also as shown in fig.16.10 below. Here the flight AB has a larger span. So it is economical to provide an intermediate support C. It should be noted that hogging moments will be produced at these intermediate supports. So top steel will have to be provided. A video of a small scale experiment, showing the behaviour of continuous systems can be seen here.
Fig.16.10
Example of a continuous support within a single flight
Effective span of stairs
Based on cl.33.1(a) of the code, the effective span l of the slabs in our case is equal to the centre to centre distance between the walls/beams. This distance is measured along the horizontal direction. We need not measure it from the centre of one support to the centre of the other, along the slope of the slab. The method of measurement is shown in the fig.16.11 below:
Fig.16.11
Effective span of stairs
Our stair falls within the category of sub clause (a) because it is supported on walls/beams parallel to the risers. The sub clauses (b) and (c) of cl.33.1 gives us the method of calculating the effective span of some other types of stairs. We will discuss about them in later sections. Later, we will also see the stairs supported on walls/beams perpendicular to the risers.
For the stairs of type which span between walls/beams parallel to risers, for a preliminary design, the thickness of waist slab can be taken as l/20. If it is a continuous type of stair as shown in fig.16.9 and 16.10, then a lesser thickness l/25 can be used. Where 'l' is the effective span.
Arrangement of steps and landings
In most cases the arrangements of steps and landings will be given in the architectural drawings. The structural designer will then have to fix up the thickness of waist slab, the arrangement of reinforcements, grade of concrete etc., But in some drawings, only the space available, and a preliminary design of stairs will be given. We will then have to design all other details. Let us see how the design in our example (fig.16.3 of the previous section) was finalised.
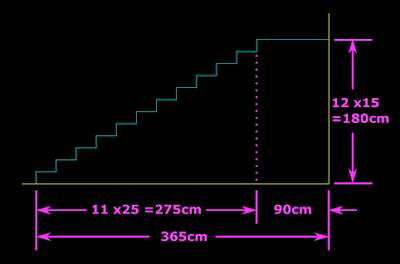
The total height that the stair has to climb is the vertical distance between the ground surface and the top of the roof slab. This is equal to 315 +45 = 360cm. If we provide two flights, the height that each flight has to climb is equal to 360/2 = 180cm. Assuming the Rise R = 15cm, the no. of Risers required for each flight = 180/15 = 12 Nos. For N Risers, there will be (N-1) Treads. So for our case, there will be 11 Treads. Assuming Tread T= 25cm, the 11 Treads will take up a length of 11 x25 = 275cm. Adding 90cm landing to this, we get 365 cm. So we can begin to draw the first riser from a point which is 365 cm from the rear end of the building. This is a vertical line 15 cm in length. It should be drawn upwards from the surface of the ground. From the top point of the first riser, a horizontal line 25 cm in length is drawn. This is the first Tread. From the end point of this line, the second riser is drawn vertically upwards. In this way, all the steps of the flight can be drawn. This is shown in the fig.16.12 below:
Fig.16.12
Outline of Risers and Treads of the first flight
Next we draw two more lines in the above diagram. The first line is the one which joins the bottom points of all risers. The second line is drawn parallel to the first line, below it, at a distance of 't' from it. Note that 't' should be measured in an exact perpendicular direction to the first line. This is shown in the fig. below:
Fig.16.13
Drawing the waist slab
The second line, upon reaching the landing will deviate, and become horizontal. It then runs parallel to the top surface of the landing at a distance of ‘t’ from it. This second line indicates the under surface of the flight.
It is clear that, in order to draw the bottom parallel line in the above fig.16.13, we must have the value of 't'. Let us see how it is calculated for the two flights. For this, we must refer figs.16.3 and 16.4. From these figs., we will get the total length of each flight and the widths of supports.
• The first flight has a total length of 365cm. The width of bottom support is 25cm and the width of top support (masonry wall) is 20cm. So the effective span = 365 -(25/2) -(20/2) = 342.5 cm
• The second flight has a total length of 90 +(11 x25) +90 = 455 cm. The width of both the supports are 20cm. So the effective span = 455 -20 =435cm.
• The second flight has more effective span. So we will calculate 't' based on it. Thus t = 435/20 = 21.75 cm.
• This can be rounded off to 22cm thickness. For uniformity, this thickness should be provided for both the flights.
• This can be rounded off to 22cm thickness. For uniformity, this thickness should be provided for both the flights.




It would be very nice if illustrative examples are also provided.....Anyway this informations are very much useful
ReplyDeleteVery good concept
ReplyDeleteThanks for this useful information.
ReplyDeleteThanks for the information
ReplyDelete