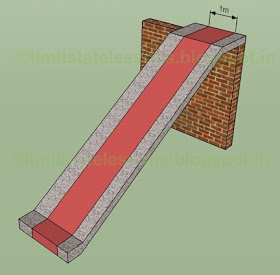
In the previous section we saw the support details and the calculation of 't'. Now we will discuss about the loads acting on the stair slabs. We know that the slabs are designed as beams of width 1m. We consider a 1 m wide strip from support to support. The same procedure is adopted for the stair slabs also as shown in the fig. below:
Fig.16.14
1m wide strip on stair slab
The width of the beam is 1m and total depth is equal to the thickness of the slab 't'. To calculate the bending moments and shear forces acting on the beam, we need to know the load acting on the beam per unit length. So another 1m is taken along the length of the strip. Thus we will get a 1 x1m square area as shown in the fig. below:
Fig.16.15
1 x1m square area on the strip
So if we have the load acting per ‘meter square area’ on the stair, we have the load acting per ‘meter length’ of the beam. This is a square area which is inclined at an angle to the horizontal. For convenience, we take the load on a 1 x1m square on the horizontal surface as shown below:
Fig.16.16
1 x1m square area on horizontal plane
We can see that the width remains the same. But the '1m length on the sloping slab' does not project exactly into '1m on the horizontal surface'. The horizontal projection will be less than 1m. This can be further illustrated using the elevation view as shown below:
Fig.16.17
Horizontal projection is always less than 1m
Let us now see how this shortage of length can be remedied while calculating the 'self wt of the slab'. From the fig.16.17 above it is clear that if we want the 'self wt of the slab' on 1m sq of horizontal area, we must take more than 1m along the slope. We must calculate this new increased length that we have to measure along the slope. For that, we will use the fig.16.18 given below:
Fig.16.18
Increased length for getting exact 1m projection
The blue colored triangle at the bottom portion, represent the step with Rise R and Tread T. We rotate this triangle through 180 degrees and then bring it under the top surface of the slab (the triangle shown within the red region). The size and shape of the triangle is not altered. Now, from similar triangles we can write
From the triangle pqr we get
From this we get
Eq.16.2
• The square root of (R2 + T2) will be always greater than T. So the value of pq will always be greater than 1.
• The weight of the concrete block colored in red will give us the self wt of the waist slab on a horizontal area of 1m2.
• This block has a length of pq and a thickness of 't'. It's width is perpendicular to the plane of the paper, and is equal to 1m. (∵ we are considering 1m wide strip for slab design).
• So the volume of the block is pq x t x 1. Multiplying this by the wt per cu.m (weight density) of reinforced concrete (25kN/m3 ), we will get the wt. of the block. So substituting for pq and multiplying by 25 we get
Eq.16.3
Self wt of waist slab on a horizontal 1m2 area (in kN/m2) =
Where R, T and t are in m
Self weight of steps
Now we will determine the self wt. of steps on a horizontal area of 1m2 . For this we will use the fig. below
Fig.16.19
Number of steps in a horizontal distance of 1m
In the calculations given below, all lengths are in m
• The number of steps in 1m length = 1⁄T Eq.16.4
• Area of cross section of one step = 1⁄2 x R x T = RT⁄2 m2.
• Length of one step, perpendicular to the plane of paper = 1m (since we are considering 1m strip for the design of slab). So volume of one step = RT⁄2 x 1 = RT⁄2 m3
• Multiplying this by the number of steps in 16.4, we will get the total volume of steps in 1m2 of horizontal area.. Thus the volume = RT⁄2 x 1⁄T = R⁄2 m3
• Multiplying this by the weight density of the material (denoted by γs ) of the steps, we will get the total weight of all the steps in 1m2 of horizontal area as given below:
Eq.16.5: Self wt of steps per 1m2 of horizontal area (in kN/m2) = (R γs) ⁄2 = 0.5Rγs. The value of γs for brick masonry is 20 kN/m3
In 16.4, we may get a whole number value if 1m is an exact multiple of T. For example if T = 0.25m, the number of steps will be 1/0.25 = 4. If T = 0.27 or 0.30 etc., we will not get a whole number. Instead we will get decimals. The decimal part indicates that 'a portion of one full step' is also coming in the 1m2 area. So we should not discard the decimal part. However we will be using 16.5 directly to calculate the self wt. In it, T, or the number of steps is not involved. So we need not be concerned about fractions of steps. In the next section, we will discuss about the other loads coming on the stairs.
Fig.16.14
1m wide strip on stair slab
The width of the beam is 1m and total depth is equal to the thickness of the slab 't'. To calculate the bending moments and shear forces acting on the beam, we need to know the load acting on the beam per unit length. So another 1m is taken along the length of the strip. Thus we will get a 1 x1m square area as shown in the fig. below:
Fig.16.15
1 x1m square area on the strip
So if we have the load acting per ‘meter square area’ on the stair, we have the load acting per ‘meter length’ of the beam. This is a square area which is inclined at an angle to the horizontal. For convenience, we take the load on a 1 x1m square on the horizontal surface as shown below:
Fig.16.16
1 x1m square area on horizontal plane
We can see that the width remains the same. But the '1m length on the sloping slab' does not project exactly into '1m on the horizontal surface'. The horizontal projection will be less than 1m. This can be further illustrated using the elevation view as shown below:
Fig.16.17
Horizontal projection is always less than 1m
Let us now see how this shortage of length can be remedied while calculating the 'self wt of the slab'. From the fig.16.17 above it is clear that if we want the 'self wt of the slab' on 1m sq of horizontal area, we must take more than 1m along the slope. We must calculate this new increased length that we have to measure along the slope. For that, we will use the fig.16.18 given below:
Fig.16.18
Increased length for getting exact 1m projection
The blue colored triangle at the bottom portion, represent the step with Rise R and Tread T. We rotate this triangle through 180 degrees and then bring it under the top surface of the slab (the triangle shown within the red region). The size and shape of the triangle is not altered. Now, from similar triangles we can write
From the triangle pqr we get
From this we get
Eq.16.2
• The square root of (R2 + T2) will be always greater than T. So the value of pq will always be greater than 1.
• The weight of the concrete block colored in red will give us the self wt of the waist slab on a horizontal area of 1m2.
• This block has a length of pq and a thickness of 't'. It's width is perpendicular to the plane of the paper, and is equal to 1m. (∵ we are considering 1m wide strip for slab design).
• So the volume of the block is pq x t x 1. Multiplying this by the wt per cu.m (weight density) of reinforced concrete (25kN/m3 ), we will get the wt. of the block. So substituting for pq and multiplying by 25 we get
Eq.16.3
Self wt of waist slab on a horizontal 1m2 area (in kN/m2) =
Where R, T and t are in m
Self weight of steps
Now we will determine the self wt. of steps on a horizontal area of 1m2 . For this we will use the fig. below
Fig.16.19
Number of steps in a horizontal distance of 1m
In the calculations given below, all lengths are in m
• The number of steps in 1m length = 1⁄T Eq.16.4
• Area of cross section of one step = 1⁄2 x R x T = RT⁄2 m2.
• Length of one step, perpendicular to the plane of paper = 1m (since we are considering 1m strip for the design of slab). So volume of one step = RT⁄2 x 1 = RT⁄2 m3
• Multiplying this by the number of steps in 16.4, we will get the total volume of steps in 1m2 of horizontal area.. Thus the volume = RT⁄2 x 1⁄T = R⁄2 m3
• Multiplying this by the weight density of the material (denoted by γs ) of the steps, we will get the total weight of all the steps in 1m2 of horizontal area as given below:
Eq.16.5: Self wt of steps per 1m2 of horizontal area (in kN/m2) = (R γs) ⁄2 = 0.5Rγs. The value of γs for brick masonry is 20 kN/m3
In 16.4, we may get a whole number value if 1m is an exact multiple of T. For example if T = 0.25m, the number of steps will be 1/0.25 = 4. If T = 0.27 or 0.30 etc., we will not get a whole number. Instead we will get decimals. The decimal part indicates that 'a portion of one full step' is also coming in the 1m2 area. So we should not discard the decimal part. However we will be using 16.5 directly to calculate the self wt. In it, T, or the number of steps is not involved. So we need not be concerned about fractions of steps. In the next section, we will discuss about the other loads coming on the stairs.






No comments:
Post a Comment