In the previous section we saw the self wt. of stair slab and the steps. Now we will see the other loads coming on the stairs.
Self weight of finishes (16.6)
The self weight of finishes applied over the steps should be considered in the design. It can be obtained from data books or relevant codes. Usually it varies from 0.5 to 1.0 kN/m2. This load obtained from data books or codes, is assumed to act vertically on a horizontal plane. So there is no need to make any modifications, and we can apply it directly.
Live Loads (16.7)
The Live loads acting on the stairs can also be obtained from the data books or relevant codes. IS 875: 1987(part II) recommends a uniformly distributed load of 5 kN/m2. This load is to be applied on both the sloping portion and the horizontal landing. In buildings such as residences, where the specified Live loads on the floors do not exceed 2 kN/m2, and the stairs are not liable to be overcrowded, the Live load can be taken as 3kN/m2. As in the case of self wt. of finishes, the LL obtained from data books or codes, is assumed to act vertically on a horizontal plane, and so there is no need make any modifications, and we can apply it directly.
Loads on Landing
The above items 16.3, 16.5, 16.6 and 16.7 are the four loads that come on the sloping slab (Going) of a flight. Let us now see the loads that come on the landing.
The landing is horizontal, and so there is no need to make any modifications for slope. The volume of a 1 x1m square block of landing slab is 1 x 1 x t = t m3. Multiplying this by the weight density of reinforced concrete will give the weight. So we get 25t kN/m2. (16.8)
• The loads coming from the finishes can be taken as the same value (16.6) that we saw for the sloping portion.
• The LL can also be taken as the same load (16.7) for sloping portion.
So we have seen all the loads coming on the stair. The loads that we determine using the above methods are characteristic loads. They must be multiplied by the appropriate load factors to obtain the factored loads.
All these loads are calculated for a 1 x1m square area. But we are considering a beam (strip of slab) of width 1m, as shown in fig.16.16. So the above load will also be the load acting on every 1m length of the beam. In other words, the load on a 1 x1 m sq. area is also the UDL acting per meter length of the beam. So we can represent our beam as shown in the fig. below:
Fig.16.20
Loads acting on the stair
In the above fig.,
Eq.16.9: w1 (Load per unit length on Sloping portion) = Load factor x {sum of values obtained from (16.3, 16.5, 16.6 and 16.7)}
Eq.16.10: w2 (Load per unit length on Landing)= Load factor x {sum of values obtained from (16.8, 16.6 and 16.7)}
Note that in Eq.16.10,
• The loads from finishes (16.6) and the LL (16.7) remains the same as that of the sloping portion.
• 16.5 is absent because there are no steps in the landing.
• 16.3 (wt. of inclined slab) is replaced by 16.8 (wt. of horizontal slab)
So w2 will have a lesser value than w1 because 16.8 will always be lesser than 16.3.
Thus we can calculate the loads and draw the diagram shown in fig.16.20 with all the details. Based on that fig., we can draw the BM and Shear force diagrams.
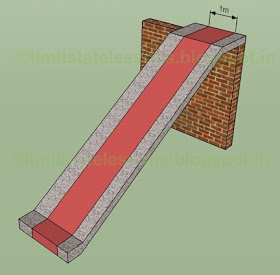
In fig.16.14 of the previous section, we have considered a strip from support to support. The fig. is shown again for convenience.
Fig.16.14
1 m wide strip
One support is a masonry wall. The other is the end of the slab which is given an increased thickness. It rests on the foundation. The strip bends between these two supports. The risers (not shown in the fig.) of this stair are all 'parallel to the two supports'. Such stairs which bend between 'supports which are parallel to the risers' are called Longitudinal stairs. The other type is the stairs which bend between 'supports which are perpendicular to the risers' are called Transverse stairs. These two types are shown schematically in the figs. below:
We will discuss about transverse stairs in later sections.
So we have a longitudinal stairs with two flights AB and CD. Flight AB has one Going and one Landing. Many times in practice, we will come across this type with one Going and one landing, which can be represented by the line diagram shown in fig.16.20 above. So it will be convenient if we derive the general equations for BM and shear forces. These equations are given below:
Reaction at support A is given by:
Eq.16.11
Reaction at support B is given by:
Eq.16.12
The bending moment at any point at a distance x from support A is given by:
Eq.16.13
If we differentiate this equation, we will get the equation for the shear force at any point at a distance x from the support. This is given below:
Eq.16.14
Maximum bending moment occurs at a place where the shear force is equal to zero. So we equate the above equation 16.14 to zero and solve for x. Then we put this value of x in 16.13 and find the value of maximum BM. The reinforcement is then designed for this maximum BM.
We have just seen the procedure for the analysis and design of a flight with one Going and one Landing. Now we will see the procedure for a flight with one Going and two landings. The method of calculation of loads are the same. When the loads are calculated, we can draw the line diagram as shown below:
Fig.16.21
Loads acting on a flight with one Going and two landings
The calculations of BM and SF are easy in this case because the beam and the loadings are symmetrical. (Note that, the lengths of both the landings are taken as l2. If they are not equal, there will not be symmetry). As before, we will write the equations as given below:
Reactions at supports C and D is given by
Eq.16.15
As the beam and the loadings are symmetrical, the maximum BM will be at the mid span. So there is no need to find the point where the SF is equal to zero. The maximum BM is given by:
Eq.16.16
Where l = l1 + 2l2
When the maximum bending moment is calculated, we can design the reinforcement required to resist that bending moment. So we will now do the detailed analysis and design of our stair. It is given as:
Solved example 16.1
The arrangement of bars according to the design in the above solved example is shown in the figs.16.22 and 16.23 given below:
Fig.16.22
Reinforcement details of flight AB
Fig.16.23
Reinforcement details of flight CD
For flight AB, the main bars of 12 mm dia. are provided at 250 mm c/c. For the flight CD, the main bars of 12 mm dia. are provided at 150 mm c/c. In the next section, we will discuss some details about the above two figs.
Self weight of finishes (16.6)
The self weight of finishes applied over the steps should be considered in the design. It can be obtained from data books or relevant codes. Usually it varies from 0.5 to 1.0 kN/m2. This load obtained from data books or codes, is assumed to act vertically on a horizontal plane. So there is no need to make any modifications, and we can apply it directly.
Live Loads (16.7)
The Live loads acting on the stairs can also be obtained from the data books or relevant codes. IS 875: 1987(part II) recommends a uniformly distributed load of 5 kN/m2. This load is to be applied on both the sloping portion and the horizontal landing. In buildings such as residences, where the specified Live loads on the floors do not exceed 2 kN/m2, and the stairs are not liable to be overcrowded, the Live load can be taken as 3kN/m2. As in the case of self wt. of finishes, the LL obtained from data books or codes, is assumed to act vertically on a horizontal plane, and so there is no need make any modifications, and we can apply it directly.
Loads on Landing
The above items 16.3, 16.5, 16.6 and 16.7 are the four loads that come on the sloping slab (Going) of a flight. Let us now see the loads that come on the landing.
The landing is horizontal, and so there is no need to make any modifications for slope. The volume of a 1 x1m square block of landing slab is 1 x 1 x t = t m3. Multiplying this by the weight density of reinforced concrete will give the weight. So we get 25t kN/m2. (16.8)
• The loads coming from the finishes can be taken as the same value (16.6) that we saw for the sloping portion.
• The LL can also be taken as the same load (16.7) for sloping portion.
So we have seen all the loads coming on the stair. The loads that we determine using the above methods are characteristic loads. They must be multiplied by the appropriate load factors to obtain the factored loads.
All these loads are calculated for a 1 x1m square area. But we are considering a beam (strip of slab) of width 1m, as shown in fig.16.16. So the above load will also be the load acting on every 1m length of the beam. In other words, the load on a 1 x1 m sq. area is also the UDL acting per meter length of the beam. So we can represent our beam as shown in the fig. below:
Fig.16.20
Loads acting on the stair
In the above fig.,
Eq.16.9: w1 (Load per unit length on Sloping portion) = Load factor x {sum of values obtained from (16.3, 16.5, 16.6 and 16.7)}
Eq.16.10: w2 (Load per unit length on Landing)= Load factor x {sum of values obtained from (16.8, 16.6 and 16.7)}
Note that in Eq.16.10,
• The loads from finishes (16.6) and the LL (16.7) remains the same as that of the sloping portion.
• 16.5 is absent because there are no steps in the landing.
• 16.3 (wt. of inclined slab) is replaced by 16.8 (wt. of horizontal slab)
So w2 will have a lesser value than w1 because 16.8 will always be lesser than 16.3.
Thus we can calculate the loads and draw the diagram shown in fig.16.20 with all the details. Based on that fig., we can draw the BM and Shear force diagrams.
In fig.16.14 of the previous section, we have considered a strip from support to support. The fig. is shown again for convenience.
Fig.16.14
1 m wide strip
One support is a masonry wall. The other is the end of the slab which is given an increased thickness. It rests on the foundation. The strip bends between these two supports. The risers (not shown in the fig.) of this stair are all 'parallel to the two supports'. Such stairs which bend between 'supports which are parallel to the risers' are called Longitudinal stairs. The other type is the stairs which bend between 'supports which are perpendicular to the risers' are called Transverse stairs. These two types are shown schematically in the figs. below:
 |
| Schematic diagram for Longitudinal stairs |
 |
| Schematic diagram for Transverse stairs |
We will discuss about transverse stairs in later sections.
So we have a longitudinal stairs with two flights AB and CD. Flight AB has one Going and one Landing. Many times in practice, we will come across this type with one Going and one landing, which can be represented by the line diagram shown in fig.16.20 above. So it will be convenient if we derive the general equations for BM and shear forces. These equations are given below:
Reaction at support A is given by:
Eq.16.11
Reaction at support B is given by:
Eq.16.12
The bending moment at any point at a distance x from support A is given by:
Eq.16.13
If we differentiate this equation, we will get the equation for the shear force at any point at a distance x from the support. This is given below:
Eq.16.14
Maximum bending moment occurs at a place where the shear force is equal to zero. So we equate the above equation 16.14 to zero and solve for x. Then we put this value of x in 16.13 and find the value of maximum BM. The reinforcement is then designed for this maximum BM.
We have just seen the procedure for the analysis and design of a flight with one Going and one Landing. Now we will see the procedure for a flight with one Going and two landings. The method of calculation of loads are the same. When the loads are calculated, we can draw the line diagram as shown below:
Fig.16.21
Loads acting on a flight with one Going and two landings
The calculations of BM and SF are easy in this case because the beam and the loadings are symmetrical. (Note that, the lengths of both the landings are taken as l2. If they are not equal, there will not be symmetry). As before, we will write the equations as given below:
Reactions at supports C and D is given by
Eq.16.15
As the beam and the loadings are symmetrical, the maximum BM will be at the mid span. So there is no need to find the point where the SF is equal to zero. The maximum BM is given by:
Eq.16.16
Where l = l1 + 2l2
When the maximum bending moment is calculated, we can design the reinforcement required to resist that bending moment. So we will now do the detailed analysis and design of our stair. It is given as:
Solved example 16.1
The arrangement of bars according to the design in the above solved example is shown in the figs.16.22 and 16.23 given below:
Fig.16.22
Reinforcement details of flight AB
Fig.16.23
Reinforcement details of flight CD
For flight AB, the main bars of 12 mm dia. are provided at 250 mm c/c. For the flight CD, the main bars of 12 mm dia. are provided at 150 mm c/c. In the next section, we will discuss some details about the above two figs.





Many Thanks bro
ReplyDeleteDetailed analysis and design link failed i wish give me another link.
ReplyDeleteAnd i want to make sure about moment and shear values because the formulas is written above based on the assumption that the flight is horizontal and ignore the reaction in x-direction this is true or not !
And thank you very much for this complete and informative presentation
Glad to know that the notes are helpful. 'detailed analysis and design' is an anchor link. Please click on 'Solved example 16.1' just below it.
DeleteStair renovation Wow, cool post. I'd like to write like this too - taking time and real hard work to make a great article... but I put things off too much and never seem to get started. Thanks though.
ReplyDelete