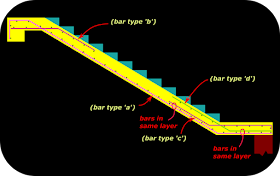
In the previous section we saw the arrangement of the stair in plan and sectional elevation views. We calculated the loads also. It appears as an ordinary longitudinal stair. In this section we will see how the load distribution is modified when the flight is given an embedment into the side wall. Later in this section, we will begin our discussion about 'transverse stairs'.
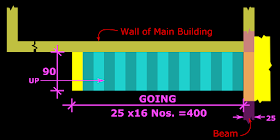
From the figs. in the previous section, we can see that the load on the Going is transferred to the ground at the bottom end and to the beams at the top end. But if the waist slab of the Going have some embedment into the side wall of the main building, then some load will be transferred to that wall also. Cl.33.2 of the code gives us the details about the load distribution when such an embedment is provided. For this clause to be applicable, the embedment that is provided, should not be less than 11 cm. Consider the modified plan of the stair given below:
Fig.16.47
Modified plan
The waist slab has an embedment of 12 cm into the wall of the main building. As this is greater than 11cm, we can apply the clause to the stair. The section xx is given in fig.16.48 below. This sectional view helps to calculate the loads based on the clause.
Fig.16.48
Section XX
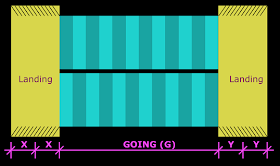
We know that the load is acting on the whole width 'W' cm of the stair (W =90cm for our stair). But when a minimum embedment of 11cm is provided, the load is assumed to act on a reduced width of (W – 15cm). This is shown in the fig.16.48 above.
Let us see how we can apply this to our stair:
We have calculated a load of 20.16 kN/m2 on the Going. If there is no embedment, the total load on the whole area of the Going will be equal to 20.16 multiplied by the total area of the Going. This is equal to 20.16 x 0.9 x 4.0 = 72.576 kN. (here 4.0 is the effective span of the Going)
As there is an embedment of 12 cm in our case, the total load can be modified as 20.16 x (0.9 – 0.15) x 4.0 = 60.48 kN. [Where (0.9 – 0.15) is the reduced width]. So we can discard 72.576 and use 60.48 kN.
Now, one more modification have to be made:
When a normal longitudinal stair bends, the width that resists the bending is W. But when the embedment mentioned above is available, the effective width of the stair, that resists the bending can be assumed to have an increased value. According to the code, this increased value is (W + 0.075). This is also shown in the fig.16.48 above.
So the load is acting on an area of [(W +0.075) x effective span ]. Thus, dividing the total load by this new area will give us the new load per 1 x 1 m square area. In our case, this is equal to 60.48 / [(0.9 + 0.075) x 4.0] = 15.51 kN/m2. So for the analysis and design, we can use a UDL of 15.51 kN/m instead of 20.16 kN/m.
The difference is transferred to the side wall. In our case, the wall is resting on the ground. So there is foundation to take up this extra load coming on the wall. But if the wall is resting on a beam, then that beam will have to be designed for an additional UDL per meter length. In our case, this additional load = 20.16 - 15.51 = 4.65 kN/m. [The landing portion of our stair does not have any such embedment. So no modification needs to be applied to the load on the landing].
It should also be noted that, this method of giving an embedment in the side wall for a longitudinal stair causes construction difficulties, and so, it is not generally used in practice.
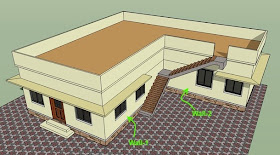
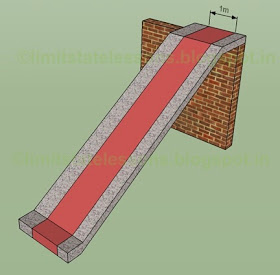
We have already seen a schematic diagram of a transverse stair here. Now we will discuss the detailed analysis and design procedure. The fig.16.49 below shows the view of an office building. It has a Basement floor, Ground floor and a First floor. The floor level of the Ground floor is at some height above the surrounding Ground surface. So a stair is provided for the access to the ground floor. Also there is open space between the basement of the building and the surrounding earth. So the stair acts as a 'bridge' also.
Fig.16.49
Example of a Transverse stair
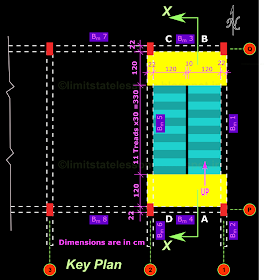
The next fig.16.50 below shows the details of the stair. A portion of the earth filling below the Ground level is removed to get a clear picture. A portion of the stair is also removed to see the waist slab.
Fig.16.50
Detailed view of Transverse stair
We can see that the brick work of the steps is resting on the waist slab. The waist slab is resting on two beams on the sides of the stair. These beams are called stringer beams. Each of the stringer beams are resting on columns:
• Column in the retaining wall support the lower end of the stringer beam
• Column in the main building support the upper end of the stringer beam
• The waist slab spans between the two stringer beams.
So the waist slab spans in a direction, which is perpendicular to the direction of travel of the pedestrians. In other words, the span is in the direction of the transverse axis of the stair. So this is a transverse stair.
The slab is simply supported on the two beams, and the span can be taken as the center to center distance between the two beams. [Though it is assumed to be simply supported, some top steel should be provided at supports to resist any hogging moments that may develop]. We have already discussed the design of beams earlier. So, in our present discussion, we are concerned with the analysis and design of the waist slab only.
It may be noted that, in the above views, finishing works are not yet applied on the stairs, while the main building is shown in a finished condition. So the brick works for the steps have to be done in such a way that, when the tile is laid on the top most step, it's top surface will be in the same level as the top surface of the tile of the floor of the main building. In the next section, we will see more details about this stair.
From the figs. in the previous section, we can see that the load on the Going is transferred to the ground at the bottom end and to the beams at the top end. But if the waist slab of the Going have some embedment into the side wall of the main building, then some load will be transferred to that wall also. Cl.33.2 of the code gives us the details about the load distribution when such an embedment is provided. For this clause to be applicable, the embedment that is provided, should not be less than 11 cm. Consider the modified plan of the stair given below:
Fig.16.47
Modified plan
The waist slab has an embedment of 12 cm into the wall of the main building. As this is greater than 11cm, we can apply the clause to the stair. The section xx is given in fig.16.48 below. This sectional view helps to calculate the loads based on the clause.
Fig.16.48
Section XX
We know that the load is acting on the whole width 'W' cm of the stair (W =90cm for our stair). But when a minimum embedment of 11cm is provided, the load is assumed to act on a reduced width of (W – 15cm). This is shown in the fig.16.48 above.
Let us see how we can apply this to our stair:
We have calculated a load of 20.16 kN/m2 on the Going. If there is no embedment, the total load on the whole area of the Going will be equal to 20.16 multiplied by the total area of the Going. This is equal to 20.16 x 0.9 x 4.0 = 72.576 kN. (here 4.0 is the effective span of the Going)
As there is an embedment of 12 cm in our case, the total load can be modified as 20.16 x (0.9 – 0.15) x 4.0 = 60.48 kN. [Where (0.9 – 0.15) is the reduced width]. So we can discard 72.576 and use 60.48 kN.
Now, one more modification have to be made:
When a normal longitudinal stair bends, the width that resists the bending is W. But when the embedment mentioned above is available, the effective width of the stair, that resists the bending can be assumed to have an increased value. According to the code, this increased value is (W + 0.075). This is also shown in the fig.16.48 above.
So the load is acting on an area of [(W +0.075) x effective span ]. Thus, dividing the total load by this new area will give us the new load per 1 x 1 m square area. In our case, this is equal to 60.48 / [(0.9 + 0.075) x 4.0] = 15.51 kN/m2. So for the analysis and design, we can use a UDL of 15.51 kN/m instead of 20.16 kN/m.
The difference is transferred to the side wall. In our case, the wall is resting on the ground. So there is foundation to take up this extra load coming on the wall. But if the wall is resting on a beam, then that beam will have to be designed for an additional UDL per meter length. In our case, this additional load = 20.16 - 15.51 = 4.65 kN/m. [The landing portion of our stair does not have any such embedment. So no modification needs to be applied to the load on the landing].
It should also be noted that, this method of giving an embedment in the side wall for a longitudinal stair causes construction difficulties, and so, it is not generally used in practice.
Transverse Stairs
We have already seen a schematic diagram of a transverse stair here. Now we will discuss the detailed analysis and design procedure. The fig.16.49 below shows the view of an office building. It has a Basement floor, Ground floor and a First floor. The floor level of the Ground floor is at some height above the surrounding Ground surface. So a stair is provided for the access to the ground floor. Also there is open space between the basement of the building and the surrounding earth. So the stair acts as a 'bridge' also.
Fig.16.49
Example of a Transverse stair
The next fig.16.50 below shows the details of the stair. A portion of the earth filling below the Ground level is removed to get a clear picture. A portion of the stair is also removed to see the waist slab.
Fig.16.50
Detailed view of Transverse stair
We can see that the brick work of the steps is resting on the waist slab. The waist slab is resting on two beams on the sides of the stair. These beams are called stringer beams. Each of the stringer beams are resting on columns:
• Column in the retaining wall support the lower end of the stringer beam
• Column in the main building support the upper end of the stringer beam
• The waist slab spans between the two stringer beams.
So the waist slab spans in a direction, which is perpendicular to the direction of travel of the pedestrians. In other words, the span is in the direction of the transverse axis of the stair. So this is a transverse stair.
The slab is simply supported on the two beams, and the span can be taken as the center to center distance between the two beams. [Though it is assumed to be simply supported, some top steel should be provided at supports to resist any hogging moments that may develop]. We have already discussed the design of beams earlier. So, in our present discussion, we are concerned with the analysis and design of the waist slab only.
It may be noted that, in the above views, finishing works are not yet applied on the stairs, while the main building is shown in a finished condition. So the brick works for the steps have to be done in such a way that, when the tile is laid on the top most step, it's top surface will be in the same level as the top surface of the tile of the floor of the main building. In the next section, we will see more details about this stair.