In the previous section we saw the conditions for providing splices. We also saw the precautions to be taken while giving splices. In this sections we will discuss some code provisions which are related specifically to lap splices.
• The sub clause (a) of this clause is related to the lap splices of bars larger than 36 mm in dia. We have already discussed about it with the help of figs.14.39 and 14.40.
• The next sub clause (b) is about ‘staggering of laps’. We shall discuss about it after seeing the sub clause (c).
Cl.26.2.5.1(c)
When the bar is under flexural tension, (a discussion on the difference between flexural tension and direct tension is given here) the lap length (fig.14.48) should not be less than the largest of the following:
(a) Ld
(b) 30Ф
Here Ld is the unique value of development length that we saw earlier.
Fig.14.48
Lap length in Flexural tension
Fig.14.49
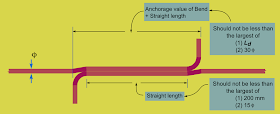
Lap length in flexural tension when hooks are provided
We have discussed about the anchorage value of hooks and bends in a previous section, and we know that it is equal to 16Ф for hooks. So this can be added to the 'straight length’ of the lap.
• Thus the 'Total contribution' [A] = 'Straight length' [B] + 16Ф. [C]
• [A] should not be less than the largest of
♦ Ld
♦ 30Ф
• [B] should not be less than the largest of
♦ 200 mm
♦ 15Ф
So we have to simultaneously check two parameters [A] and [B] and ensure that they do not fall below required values. These requirements are clearly shown in the fig.14.49
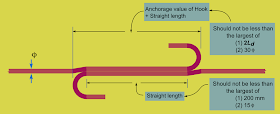
This same fig. can be used for bends also, just by changing the hooks to bends. Also, in the calculations, the anchorage value should be taken as 8Ф. All the other details remain the same. It is shown in fig.14.50 below:
Fig.14.50
Lap length in flexural tension when bends are provided
• Thus the 'Total contribution' [A] = 'Straight length' [B] + 8Ф. [C]
• [A] should not be less than the largest of
♦ Ld
♦ 30Ф
• [B] should not be less than the largest of
♦ 200 mm
♦ 15Ф
So we have to simultaneously check two parameters [A] and [B] and ensure that they do not fall below required values. These requirements are clearly shown in the fig.14.50
Next we will see the lap length requirements when the bar is in 'direct tension'. In fact, with a small modification, the above three figures can be used to show the lap length requirements in direct tension also. The modification is that, 2Ld is to be used in place of Ld when direct tension is considered. Thus, corresponding to the above three figs.14.48, 14.49 and 14.50, we get the three figs.14.51, 14.52 and 14.53 given below:
Fig.14.51
Lap length in Direct tension
Fig.14.52
Lap length in Direct tension when hooks are provided
• 'Total contribution' [A] = 'Straight length' [B] + 16Ф. [C]
• [A] should not be less than the largest of
♦ 2Ld
♦ 30Ф
• [B] should not be less than the largest of
♦ 200 mm
♦ 15Ф
So we have to simultaneously check two parameters [A] and [B] and ensure that they do not fall below required values. These requirements are clearly shown in the fig.14.52
Fig.14.53
Lap length in Direct tension when bends are provided
• 'Total contribution' [A] = 'Straight length' [B] + 8Ф. [C]
• [A] should not be less than the largest of
♦ 2Ld
♦ 30Ф
• [B] should not be less than the largest of
♦ 200 mm
♦ 15Ф
So we have to simultaneously check two parameters [A] and [B] and ensure that they do not fall below required values. These requirements are clearly shown in the fig.14.53
The clause which we are discussing now is the sub clause (c) of 26.2.5.1. It gives us the guidelines for calculating the lap length. We have seen the details above.
Now, this sub clause in turn, have two sub clauses. Sub clause (1) and sub clause (2). These sub clauses gives us the guidelines for 'increasing the lap length' when the concrete cover provided for the steel bars are below certain specified values.
This can be explained as follows: We know that, for the lapped splice to work properly, sufficient bond should develop between steel and concrete. So there must be sufficient 'mass of well compacted concrete' all around the bars. The 'inner bars' of various members will have sufficient concrete all around. But the bars which are near the exposed surfaces will be having only limited concrete (which we denote as the concrete cover) on the exposed side. This is a cause for concern. If the concrete cover is below certain specified values, an increase in lap length is required. The sub clauses (1) and (2) give the guidelines for this increase. We will discuss about them with the help of an example. Consider the continuous beam shown in the fig.14.54 below:
Fig.14.54
Sectional Elevation of a continuous beam
Fig.14.55
Cross sectional views
Consider the sectional view XX. This section shows the bars at the midspan region. We can see that, there are 3 bars at the top. These bars are named as a, a' and b. We know that at the intermediate support of a continuous beam, there will be hogging moment, and so, these three top bars will be in tension. If the cover ct at the top is less than twice the diameter of the bar, then each of these bars is an example of the bar specified in the sub clause (1). So if lapped splices need to be provided for these types of bars, and ct is less than 2Ф, we must take the following steps:
• First, find L by following the 'rules for obtaining the lap length for bars in flexural tension' that we discussed above. (Figs.14.48 to 14.50).
• Then obtain the modified value by multiplying this L by 1.4.
This modified value should be provided for the lap. The need for such an increase in the lap length can be explained as follows:
When concrete is poured into the member, and compacted at the time of casting, water and air will rise towards the top of the concrete mass, and will get trapped at the under side of the horizontal reinforcement. This will weaken the bond between steel and concrete. So we must increase the lap length.
The sub clause 26.2.5.1.c (1) that we discussed above is specifically intended for top bars of a beam. All the top bars will be having a top cover of ct. It is the value of this ct which will determine whether this sub clause (1) is applicable to the top bar under consideration.
But the top bars will be having cover from sides and bottom also. How do these covers affect the lap length calculations?
• Bottom covers: We know that, the bottom covers of the top bars will be large. So they do not cause much concern.
• Side covers: If slab is present at the top portion of the beam, so as to form a T-beam, then side bars a and a' will also be having large covers. The middle bar b will be having enough side covers whether or not it is a T-beam.
♦ But if it is not a T-beam, the side covers for a and a' will also cause concern. Then some other clauses (which we will discuss soon) will also be applicable to a and a'.
So in general, if a bar is such that, only the sub clause (1) is applicable (for computing required increments in lap lengths based on covers), then:
■ It should be a top bar
■ Only ct should cause concern.
■ cb and cs should be sufficiently large so as not to cause any concern.
Next we consider the section YY. This section shows the bars at the midspan region. We can see that there are 3 bottom bars in the midspan region. These bars (named as c, c' and d) will be in tension. Consider the corner bars c and c'. These two bars have clear cover from two faces. The side vertical face, and the bottom horizontal face of the beam. These covers are denoted as cs and cb. If any of these covers is less than 2Ф, then these two bars are examples of the bars specified in the sub clause (2). So if lapped splices need to be provided for any of these two bars, we must take the following steps:
• First, find L by following the 'rules for obtaining the lap length for bars in flexural tension' that we discussed above. (Figs.14.48 to 14.50).
• Then obtain the modified value by multiplying this L by 1.4.
The sub clause 26.2.5.1.c (2) that we discussed above is specifically intended for corner bars of a beam. All the corner bars will be having two covers:
• The cover from top horizontal surface ct (if it is a top corner bar) or the cover from bottom horizontal surface cb (if it is a bottom corner bar).
• The cover from the exposed vertical side cs
Both these values should be checked. If any of the two is less than 2Ф, then this sub clause is applicable to that bar.
It may be noted that, if it is not a T-beam, the top bars a and a' will also be corner bars.
This sub clause (2) gives specifications for some other situations also. We will see them in the next section.
Copyright©2016 limitstatelessons.blogspot.com - All Rights Reserved






No comments:
Post a Comment