In the previous sections we completed the discussion on the methods to determine the theoretical cut-off points. We saw the exact method as well as the approximate method. Both the methods give us 'theoretical points'. As mentioned earlier, the bars should not be stopped at these theoretical points. They must be continued further. This means that the 'actual' cut-off points will be different from the 'theoretical' ones.
One of the obvious reasons for not accepting the theoretical points can be stated as follows: We have used the BM diagrams for calculating the points. But these diagrams can undergo unexpected changes. These unexpected changes may occur due to changes in loads, changes in positions of Live loads, sinking of supports etc., So the points obtained from BM diagrams cannot be relied upon. In this and the following sections, we will explore more reasons for continuing the bars beyond the theoretical points, and also 'how much' further we have to take the bars.
One of the obvious reasons for not accepting the theoretical points can be stated as follows: We have used the BM diagrams for calculating the points. But these diagrams can undergo unexpected changes. These unexpected changes may occur due to changes in loads, changes in positions of Live loads, sinking of supports etc., So the points obtained from BM diagrams cannot be relied upon. In this and the following sections, we will explore more reasons for continuing the bars beyond the theoretical points, and also 'how much' further we have to take the bars.
Consider a simply supported beam. When the factored load is applied on the beam, flexural cracks (‘flexural cracks’ means the cracks formed due to the bending of the beam) will be first appearing in the midspan region as shown in the fig.15.19 below:
Flexural cracks appearing at midspan region
Also, the midspan section will reach the ultimate state. That is., the steel at the midspan section will yield, and the concrete strain at that section will become 0.002. While the midspan section is undergoing these changes, other sections which are at some distance away from the midspan will still be in a safe condition. This is because, these other sections have a 'capacity' (we measure this ‘capacity’ in terms of the ultimate moment of resistance, MuR) which is greater than the applied factored bending moment at these sections.
But when we do 'curtailment of bars', the section or sections at which the curtailment is done, will also become critical sections. This is because, the applied factored bending moment at a section where curtailment is done, will be comparable to the capacity of the section. At such sections flexural cracks will begin to form as shown in the fig.15.20 below:
Fig.15.20
Flexural cracks appearing at a section XX at which curtailment is done
These flexural cracks may develop into diagonal tension cracks as shown in the fig.15.21 below. The possibility of formation of such diagonal cracks is high if heavy shear force is present near the section at which curtailment is done.
Fig.15.21
Flexural cracks developed into a diagonal tension crack
We will now analyse the forces in this cracked beam. For this, we will first look at an ordinary un-cracked beam shown in fig.15.22 below.
Fig.15.22
Simply supported beam with a factored udl of wu kN/m
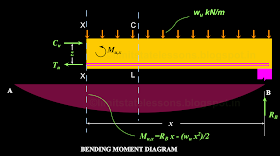
From the basic lessons of strength of materials, we know how to calculate the applied bending moment at any section XX, at a distance 'x' from either support. We draw a free body diagram of the portion on the right of section XX. This is shown in the fig.15.23 below:
Fig.15.23
Free body diagram of the portion to the right of XX
• The moment at XX, due to the reaction RB is equal to RB x (anti-clock wise).
• The moment at XX due to the applied load wu is equal to (wu x2 )/2 (clock wise)
• So the net factored moment at XX is given by:
Mu,x = RB x – (wu x2 )/2
This equation will give us the applied factored bending moment at any section. Now we can look into the internal forces as shown in the fig.15.24 below:
Fig.15.24
Equilibrium of internal forces
• The tensile force Tu acts at the centroid of the steel area.
• These two forces are equal in magnitude but opposite in direction. So they form a couple. The magnitude of this couple is equal to Tu z . It is also equal to Cu z . Here, z is the lever arm.
• This couple resists the applied factored bending moment Mu,x.
So now we know the details about the internal forces. We can use the same procedure for analysing the internal forces in the cracked beam shown in fig.15.19 above. We will discuss about it in the next section.
Copyright©2016 limitstatelessons.blogspot.com - All Rights Reserved





No comments:
Post a Comment