In the previous section we saw the critical sections for shear design in different structural members. Now we will do the complete shear design of a beam.
Solved example 13.1
A rectangular beam is 400 mm wide and it’s effective depth is 550 mm. It is simply supported on two masonry walls, each of 300 mm thickness. The center to center distance between the supports is 6000 mm. The beam carries a factored UDL of 135 kN/m. The tensile steel of the beam has an area of 3927 mm2. This steel continues uninterrupted from support to support. Determine the diameter and spacing of vertical stirrups to resist the shear force applied on the beam. Assume Fe 415 steel and M25 concrete.
Solution:
We will write down the given data:
b =400 mm, d =550 mm, Ast =3927.00 mm2, fy =415 N/mm2, fck =25 N/mm2, c/c Distance between supports =6000 mm, Widths of supports =300 mm.
We have to calculate the effective span (l) of the above beam.
Clear span cs = 6000-300 =5700
• cs + d = 5700 + 550 = 6250 mm
• c/c distance between supports = 6000 mm
Lesser of the above = l= 6000 mm
So the SF and BM diagrams should be drawn for a distance of 6000 mm from the center of one support to the center of the other.
A UDL of 135 kN/m is applied on the beam. When we design this beam for flexure, we will obtain a doubly reinforced section. However, the details of the flexure design of the beam is not discussed here. For shear design, we need the quantity of tensile steel, and it is given to us as Ast = 3927 mm2.
The details of shear design is given below:
First of all, we have to check if the condition Vu ≤ VuR is satisfied
For our beam, maximum shear force Vu will be at the support, and it is equal to the support reaction =405 kN
VuR,lim = τc,max bd
From table 20 of the code, for M25 concrete, τc,max =3.1 N/mm2
Thus we get VuR,lim =682000 N =682 kN. This is greater than Vu. Hence OK
We have used the maximum possible value (the support reaction) of Vu for the above check. For the design of stirrups, we will be using a lesser value (the shear force at the critical section, which is at a distance d from the face of the support) of Vu. The check is satisfied for the maximum possible value. So it will be satisfied for the Vu at critical section also. So we can proceed with the design.
We will now draw the Shear force diagram for the beam:
The data required for drawing the SF diagram are the following:
Total Factored udl =wu =135 kN/m
Effective span =l =6000 mm
In the above diagram, points A and C have a 'y' coordinate of 405 kN, which is the support reaction.
It may be noted that the equation of the above shear force plot is: y =405 -135x - - - (1)
• 405 is the support reaction
• 135 is the udl
Now we will consider Vuc, the contribution from concrete:
The bottom tensile steel is given uninterrupted from support to support. So Ast will be the same at whichever section that we take. This means that the shear stress contributed by concrete will be the same at whichever section that we take. So the graph of Vuc will be a horizontal line.
We have Vuc =τcbd (Details here). We have to calculate τc. For this, we look at table 19 of the code.
pt = 100Ast/bd =1.785
1.750 → 0.7800
1.785 → 0.7856
2.000 → 0.8200. So we get τc =0.7856 N/mm2.
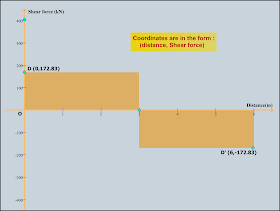
Thus Vuc = 172,832.000 N =172.832 kN
In the above diagram, points D and D' have a 'y' coordinate of 172.832 which is the value of Vuc.
It may be noted that the equation of the above plot is:
• y =172.83 upto the mid span and
• y = -172.83 from the mid span to the end support.
In the above fig., the point of intersection of the two plots is at 'E'. 'E' has a y coordinate of 172.83. This we can obtain without any calculations because 'E' lies on the plot of Vuc, on which all points have same y value
Now we will find the x coordinate. For this, we put the above value for 'y' , and solve for 'x' in the equation (1) for Vu that we wrote earlier:
y =405 -135x
Solving we get x = 1.720 m
Another method is to use similar triangles AOB and ADE as shown:
After point E, the applied shear force Vu becomes less than Vuc.
We can see that the beam is symmetrical about the midpoint. So we need to consider only one half for the shear design. This will give us more space to work on. So the above fig. is modified as shown below:
We can see that the beam is symmetrical about the midpoint. So we need to consider only one half for the shear design. This will give us more space to work on. So the above fig. is modified as shown below:
[It may be noted that, we are able to work with one half of the span because the beam is symmetrical, and the loading is also symmetrical. These conditions may not be obtained always. For example, if in a continuous beam, the spans are unequal and/or the loading is unequal, we will not be able to get a symmetrical BM and SF diagram.]
Now we look at the critical section of the above beam. The critical section is at a distance of d from the face of the support. The support details are shown below:
For our beam, the effective span is the c/c distance between supports. So the SF diagram is drawn from center of one support to the center of other. From the above fig., we can see that the distance of the critical section from the left end of the SF diagram is equal to 0.15 + 0.55 = 0.70
The portion between A and F need to be designed for 310.5 kN only.
Before calculating the spacing of stirrups for the above Vu of 310.5 kN, We will work out the constraints that have to be considered.
The first constraint that we have to calculate is:
Portions of our beam for which stirrups should be compulsorily provided. (details here)
So we have to make a plot of 0.5Vuc and super impose it on the above graph. This is shown in the fig. below:
'G' has a y coordinate of 86.42. This we can obtain without any calculations because 'G' lies on the plot of 0.5Vuc, on which all points have same y value.
Now we find the x coordinate. For this, we put the above value for 'y' , and solve for 'x' in the equation (1). Solving we get x = 2.360 m.
From the above graph, we can make the following inferences:
• The concrete of the beam section can take up the shear beyond point E.
• So theoretically there is no need to provide stirrups beyond E.
• But the code does not allow us to do so. According to the code, we must provide stirrups even beyond E, upto point G.
The amount of stirrups required from E to G can be obtained from:
Assuming 2 legged 8mm dia. stirrups, Asv = 100.53 mm2
Substituting in the above expression, we get Sv should be less than or equal to 226.85 mm - - - (2)
The code does not require us to provide stirrups in the region from G to B. But it is a good design practice to provide stirrups there also.
The maximum spacing of stirrups allowed by the code.
Spacing should not be more than the smallest of the following:
(a) 0.75d =412.5 mm
(b) 300 mm
Comparing with (2), we can say that, the spacing at any point of the beam should not be less than 226.85 mm








No comments:
Post a Comment