In
the previous section we completed the analysis of a T-beam section. In this section we will see the analysis of another T-beam section.
Solved Example 9.2:
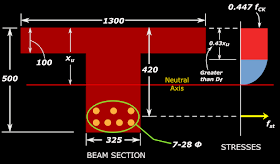
Calculate the Ultimate moment of resistance MuR of the T-beam section given in fig.9.22 below:
Fig.9.22
Section of T-beam
Assume fck = 20 N/mm2 and Fe 415 steel.
Solution:
We will first write the following data:
bf =1300 mm, Df =100 mm, D =500 mm, bw =325 mm, d =420 mm, Ast =4310.27 mm2 (7-28Ф)
For Fe415 steel, xu,max / d = 0.4791 (Table 3.4)
So xu,max for our beam section = 0.4791 x 420 =201.22 mm - - - - (1)
Now we can start the analysis procedure:
We know that the given beam section may fall into any of the three cases shown in fig.9.17. To find xu and MuR, we first need to know the particular case into which our beam will fall. For this, we have to do some tests.
The first test will be to check whether the beam falls into the category of 'Case 1: Df ≥ xu'. For doing this test, we have to make the following assumption:
• xu has the maximum value possible within case 1.
This maximum possible value is equal to Df. So we put xu = Df =100 mm
We need to get a good understanding about this assumption. We can see a '≥' symbol in the name of this case 1. This means that xu can have a value less than or equal to Df. The maximum value possible is Df. In the above assumption, we are giving this maximum possible value to xu. In this situation, the stress distribution will be as shown in the fig.9.23 below:
Fig.9.23
Stress distribution when xu = Df
In the above fig., xu = 100 mm. So the NA coincides with the bottom edge of the flange.
• Also, when we assume the above value for xu, it automatically implies that: 'we are assuming the section to be under reinforced'. This is because, the value of 100 mm for xu is less than xu,max which is obtained in (1)
If the above two assumptions that we make are true, at ultimate state, the compressive force in concrete will be equal to
Cu = 0.362 fck bf xu = 941200 N
Note that the above equation is obtained by changing b to bf in Eq.3.7
And the tensile force in steel (steel would have yielded at ultimate state if it is an under reinforced section) will be equal to
Tu = 0.87fy Ast = 1556222.98 N
From the above results, we find that Cu is less than Tu. This is not allowable. So we want an increased value for Cu. Let us assess this situation:
• If we want an increased value of Cu, then concrete area should be increased.
• This will imply that the position of NA should be lowered, which is same as saying: value of xu should increase.
• But we have already given the maximum possible value of xu in Case 1.
• If we further increase xu, then, Point 'A' in the above fig.9.23 will fall in the web, and it will no longer be Case 1
• This will imply that our beam is beyond the limits of case 1.
Thus we discard Case 1 and try 'Case 2(1)'. We do a test to check whether the beam falls into the category of 'case 2(1): Df < xu AND Df ≤ 0.43xu'. For doing this test, we have to make the following assumption:
• The height (0.43xu) of the rectangular portion of the stress block (coloured in red) has the smallest value possible within case 2(1).
This smallest possible height of the red block is equal to Df. So we put 0.43xu = Df =100 mm. Which gives xu = 100/0.43 = 232.56 mm.- - - (2)
We need to get a good understanding about this assumption. We can see a '≤' symbol in the name of this case. This means that 0.43xu can have a value greater than or equal to Df. The smallest value possible is Df. In the above assumption, we are giving this smallest possible value to 0.43xu. In other words, we are giving the smallest possible value of 100 mm for the 'height of the red block'. In case 2(1), the red block cannot get any smaller than this. In this situation, the stress distribution will be as shown in the fig. below:
Fig.9.24
Stress distribution when 0.43xu = Df
• Also, when we assume the above value for 0.43xu, it automatically implies that we are 'assuming the section to be over reinforced'. This is because, the value of 232.56 mm (obtained in (2) above) for xu is greater than xu,max which is obtained in (1)
If the above two assumptions that we make are true, at ultimate state, the compressive force in concrete will be equal to
Eq.9.12
Cuw + Cuf = Cu = 0.362fck bw xu + 0.447fck Df (bf -bw) = 1438329.6 N
But the calculation of Tu is not so easy. This is because xu is greater than xu,max. We have to first calculate the stress in steel. For this, we will have to use the strain compatibility method. We have earlier used this method for the analysis of an over reinforced 'rectangular section'. It can be seen here.
Eq.3.19
= 0.002821
From the table for Fe 415 steel we get:
So we will get Tu = fst x Ast = 352.33 x 4310.27 =1518637.43 N.
What we did in the above strain compatibility method can be simply explained as follows:
• We have a value of xu =232.56 mm. Unfortunately, this is greater than xu,max.
• So if 232.56 mm is indeed the value of xu at the ultimate state, steel will not yield at the ultimate state. If steel does not yield, we cannot say that the stress in it is 0.87fy.
• Instead, we have to calculate the stress by using strain compatibility. That is., we first calculate the strain corresponding to the xu value of 232.56 mm. This we do using Eq.3.19 above.
• Then we calculate the stress corresponding to this strain. This we do by using linear interpolation between values from the table for Fe 415 steel.
We find that Cu is still lesser than Tu. This will not give equilibrium. So we want an increased value for Cu.
Here, we must do some simple calculations to decide which way to proceed. We have earlier discarded Case 1. We are now in case 2(1). We have to check whether there is any possibility by which we can remain in this case 2(1):
• We find that Cu is lesser than Tu, which means, we have to increase the value of xu. This is to increase Cu. This means that point 'A' in the above fig.9.20 must move downwards.
• When 'A' moves downwards, xu will surely increase, and along with that, '0.43xu' will also decrease. That is., point 'B' will also move downwards. This will mean that the height of the red block will be greater than Df. So we will still remain in case 2(1).
• We can say this: The situation demands us to increase xu. This increase enables us to remain in case 2(1)
• Now we must check whether there is any possibility that the beam section will ever fall into the one remaining case, which is 'case 2(2).
• We can analyse it in this way: If the section is to fall into case 2(2), 0.43xu must decrease from the present value of 100mm.
• But if we decrease it's value, xu will also decrease, and there by, Cu will also decrease.
• We are trying to increase Cu, to make it equal to Tu.
• So the beam section can never fall into case 2(2) under any circumstances.
[In the above steps we must think of another possibility. We said that we want to increase xu, so that Cu will increase and become equal to Tu. This is because Tu is now at a higher value than Cu, and we want to bring Cu to that level. And so, 'we must increase xu, and with this increase, we will remain in case 2(1)'. But this would also mean that: 'if Tu decreases, we can move the NA upwards, thus decreasing xu, and the section will fall in case 2(2)'. Let us verify this possibility. We will use the fig. below:
The fig. shows three positions of the NA. We can see that as the NA moves upwards, the strain εst in steel is increasing. So in our case, if we move the NA upwards, the strain in steel will increase from the present value. So stress will also increase. Thus the force Tu will increase. This will necessitate the down ward movement of the NA, and so the possibility of falling in the case 2(2) can be ruled out.]
Thus we discard two cases. Our case is case 2(1). The calculations and discussions that we did so far in this problem were important 'Tests'. Tests to arrive at a conclusion about the case which our beam section will belong to. At the end of those tests, we conclude that our beam section belongs to 'case 2(1): Df < xu AND Df ≤ 0.43xu'
We also get another important information about the beam section: We have seen that xu must have a value greater than 232.56 mm. But this value of 232.56 is already greater than xu,max which is equal to 201.22 mm (1). So our section is indeed an over reinforced section.
Based on the above conclusions, we can proceed to calculate the MuR as if we 'already know that the section belongs to case 2(1)'. The stress distribution in the beam section will be as shown in the fig. below:
Fig.9.25
Actual stress distribution
To analyse an over reinforced section, we use strain compatibility method. We want an initial trial value of xu for the first cycle of the iteration process. This can be obtained as follows:
Let us assume the steel will yield at ultimate state. Then the force in steel would be Tu = 0.87 x 415 x 4310.27 = 1556222.98 N
Then, the force in concrete at ultimate state would be given by
Eq.9.12
Cuw + Cuf = Cu = 0.362fck bw xu + 0.447fck Df (bf -bw)
= 2353xu + 871650
Equating the two we get xu =290.94 mm
This value is shown in the fig. below:
Fig.9.26
Upper and lower limits of xu
We know that the value of 290.94 mm for xu will never be obtained in our beam section because, the steel in our section will never yield. Because before yielding, the concrete would have crushed. Thus we have two values for xu.
• A lower value of xu,max = 201.22 mm (represented by line 'p') which is 'too low' to give the required compressive force , and
• An upper value of 290.94 mm (represented by line 'q') which will never be achieved.
The actual xu will lie in between these two lines. We can take the average of these two as the initial trial value. So initial trial value = 0.5(201.22 +290.94) = 246.08 mm. With this, we can start the iteration process.
First cycle:
Step 1: Initial trial value of xu = 246.08 mm
Step 2: Eq.9.12
Cuw + Cuf = Cu = 0.362fck bw xu + 0.447fck Df (bf -bw) =1450676.24 N.
Step 3: Eq.3.19
= 0.00247
Find fst:
From the table for Fe 415 steel we get:
Step 4:
Tu = fst x Ast = 344.44 x 4310.27 =1484629.4 N.
We find that Cu in step 1 is not equal to Tu in step 4. So we have to do the process again. This time with an improved value of xu. This new improved value is obtained as follows:
(a) First find the value of xu as if the Tu obtained in the above cycle is the equilibrium force. So we can put Tu = 1484629.4 = Cu = 0.362fck bw xu + 0.447fck Df (bf -bw)
⇒ 1484629.4 = 2353xu + 871650
⇒ xu = 260.51 mm
(b) Now take the average of this value and the value of xu used in this cycle. Average value is equal to 0.5(260.51 + 246.08) = 253.3 mm. This average value is to be used as the trial value of xu in the next cycle.
Five cycles are done to complete the iteration process. It can be seen here. The first cycle that we did above, is also included in it. At the end of the fifth cycle, the value of xu obtained is 252.11 mm. We can use this value to calculate MuR.
Eq.9.11
= 509.45 kNm
This completes the analysis of the given beam section. In the next section we will see the analysis of another beam section.
PREVIOUS
Solved Example 9.2:
Calculate the Ultimate moment of resistance MuR of the T-beam section given in fig.9.22 below:
Fig.9.22
Section of T-beam
Solution:
We will first write the following data:
bf =1300 mm, Df =100 mm, D =500 mm, bw =325 mm, d =420 mm, Ast =4310.27 mm2 (7-28Ф)
For Fe415 steel, xu,max / d = 0.4791 (Table 3.4)
So xu,max for our beam section = 0.4791 x 420 =201.22 mm - - - - (1)
Now we can start the analysis procedure:
We know that the given beam section may fall into any of the three cases shown in fig.9.17. To find xu and MuR, we first need to know the particular case into which our beam will fall. For this, we have to do some tests.
The first test will be to check whether the beam falls into the category of 'Case 1: Df ≥ xu'. For doing this test, we have to make the following assumption:
• xu has the maximum value possible within case 1.
This maximum possible value is equal to Df. So we put xu = Df =100 mm
We need to get a good understanding about this assumption. We can see a '≥' symbol in the name of this case 1. This means that xu can have a value less than or equal to Df. The maximum value possible is Df. In the above assumption, we are giving this maximum possible value to xu. In this situation, the stress distribution will be as shown in the fig.9.23 below:
Fig.9.23
Stress distribution when xu = Df
In the above fig., xu = 100 mm. So the NA coincides with the bottom edge of the flange.
• Also, when we assume the above value for xu, it automatically implies that: 'we are assuming the section to be under reinforced'. This is because, the value of 100 mm for xu is less than xu,max which is obtained in (1)
If the above two assumptions that we make are true, at ultimate state, the compressive force in concrete will be equal to
Cu = 0.362 fck bf xu = 941200 N
Note that the above equation is obtained by changing b to bf in Eq.3.7
And the tensile force in steel (steel would have yielded at ultimate state if it is an under reinforced section) will be equal to
Tu = 0.87fy Ast = 1556222.98 N
From the above results, we find that Cu is less than Tu. This is not allowable. So we want an increased value for Cu. Let us assess this situation:
• If we want an increased value of Cu, then concrete area should be increased.
• This will imply that the position of NA should be lowered, which is same as saying: value of xu should increase.
• But we have already given the maximum possible value of xu in Case 1.
• If we further increase xu, then, Point 'A' in the above fig.9.23 will fall in the web, and it will no longer be Case 1
• This will imply that our beam is beyond the limits of case 1.
Thus we discard Case 1 and try 'Case 2(1)'. We do a test to check whether the beam falls into the category of 'case 2(1): Df < xu AND Df ≤ 0.43xu'. For doing this test, we have to make the following assumption:
• The height (0.43xu) of the rectangular portion of the stress block (coloured in red) has the smallest value possible within case 2(1).
This smallest possible height of the red block is equal to Df. So we put 0.43xu = Df =100 mm. Which gives xu = 100/0.43 = 232.56 mm.- - - (2)
We need to get a good understanding about this assumption. We can see a '≤' symbol in the name of this case. This means that 0.43xu can have a value greater than or equal to Df. The smallest value possible is Df. In the above assumption, we are giving this smallest possible value to 0.43xu. In other words, we are giving the smallest possible value of 100 mm for the 'height of the red block'. In case 2(1), the red block cannot get any smaller than this. In this situation, the stress distribution will be as shown in the fig. below:
Fig.9.24
Stress distribution when 0.43xu = Df
• Also, when we assume the above value for 0.43xu, it automatically implies that we are 'assuming the section to be over reinforced'. This is because, the value of 232.56 mm (obtained in (2) above) for xu is greater than xu,max which is obtained in (1)
If the above two assumptions that we make are true, at ultimate state, the compressive force in concrete will be equal to
Eq.9.12
Cuw + Cuf = Cu = 0.362fck bw xu + 0.447fck Df (bf -bw) = 1438329.6 N
But the calculation of Tu is not so easy. This is because xu is greater than xu,max. We have to first calculate the stress in steel. For this, we will have to use the strain compatibility method. We have earlier used this method for the analysis of an over reinforced 'rectangular section'. It can be seen here.
Eq.3.19
= 0.002821
From the table for Fe 415 steel we get:
| Strain | Stress |
| 0.00276 | 351.80 |
| 0.002821 | 352.33 |
| 0.00380 | 360.90 |
What we did in the above strain compatibility method can be simply explained as follows:
• We have a value of xu =232.56 mm. Unfortunately, this is greater than xu,max.
• So if 232.56 mm is indeed the value of xu at the ultimate state, steel will not yield at the ultimate state. If steel does not yield, we cannot say that the stress in it is 0.87fy.
• Instead, we have to calculate the stress by using strain compatibility. That is., we first calculate the strain corresponding to the xu value of 232.56 mm. This we do using Eq.3.19 above.
• Then we calculate the stress corresponding to this strain. This we do by using linear interpolation between values from the table for Fe 415 steel.
We find that Cu is still lesser than Tu. This will not give equilibrium. So we want an increased value for Cu.
Here, we must do some simple calculations to decide which way to proceed. We have earlier discarded Case 1. We are now in case 2(1). We have to check whether there is any possibility by which we can remain in this case 2(1):
• We find that Cu is lesser than Tu, which means, we have to increase the value of xu. This is to increase Cu. This means that point 'A' in the above fig.9.20 must move downwards.
• When 'A' moves downwards, xu will surely increase, and along with that, '0.43xu' will also decrease. That is., point 'B' will also move downwards. This will mean that the height of the red block will be greater than Df. So we will still remain in case 2(1).
• We can say this: The situation demands us to increase xu. This increase enables us to remain in case 2(1)
• Now we must check whether there is any possibility that the beam section will ever fall into the one remaining case, which is 'case 2(2).
• We can analyse it in this way: If the section is to fall into case 2(2), 0.43xu must decrease from the present value of 100mm.
• But if we decrease it's value, xu will also decrease, and there by, Cu will also decrease.
• We are trying to increase Cu, to make it equal to Tu.
• So the beam section can never fall into case 2(2) under any circumstances.
[In the above steps we must think of another possibility. We said that we want to increase xu, so that Cu will increase and become equal to Tu. This is because Tu is now at a higher value than Cu, and we want to bring Cu to that level. And so, 'we must increase xu, and with this increase, we will remain in case 2(1)'. But this would also mean that: 'if Tu decreases, we can move the NA upwards, thus decreasing xu, and the section will fall in case 2(2)'. Let us verify this possibility. We will use the fig. below:
The fig. shows three positions of the NA. We can see that as the NA moves upwards, the strain εst in steel is increasing. So in our case, if we move the NA upwards, the strain in steel will increase from the present value. So stress will also increase. Thus the force Tu will increase. This will necessitate the down ward movement of the NA, and so the possibility of falling in the case 2(2) can be ruled out.]
Thus we discard two cases. Our case is case 2(1). The calculations and discussions that we did so far in this problem were important 'Tests'. Tests to arrive at a conclusion about the case which our beam section will belong to. At the end of those tests, we conclude that our beam section belongs to 'case 2(1): Df < xu AND Df ≤ 0.43xu'
We also get another important information about the beam section: We have seen that xu must have a value greater than 232.56 mm. But this value of 232.56 is already greater than xu,max which is equal to 201.22 mm (1). So our section is indeed an over reinforced section.
Based on the above conclusions, we can proceed to calculate the MuR as if we 'already know that the section belongs to case 2(1)'. The stress distribution in the beam section will be as shown in the fig. below:
Fig.9.25
Actual stress distribution
To analyse an over reinforced section, we use strain compatibility method. We want an initial trial value of xu for the first cycle of the iteration process. This can be obtained as follows:
Let us assume the steel will yield at ultimate state. Then the force in steel would be Tu = 0.87 x 415 x 4310.27 = 1556222.98 N
Then, the force in concrete at ultimate state would be given by
Eq.9.12
Cuw + Cuf = Cu = 0.362fck bw xu + 0.447fck Df (bf -bw)
= 2353xu + 871650
Equating the two we get xu =290.94 mm
This value is shown in the fig. below:
Fig.9.26
Upper and lower limits of xu
We know that the value of 290.94 mm for xu will never be obtained in our beam section because, the steel in our section will never yield. Because before yielding, the concrete would have crushed. Thus we have two values for xu.
• A lower value of xu,max = 201.22 mm (represented by line 'p') which is 'too low' to give the required compressive force , and
• An upper value of 290.94 mm (represented by line 'q') which will never be achieved.
The actual xu will lie in between these two lines. We can take the average of these two as the initial trial value. So initial trial value = 0.5(201.22 +290.94) = 246.08 mm. With this, we can start the iteration process.
First cycle:
Step 1: Initial trial value of xu = 246.08 mm
Step 2: Eq.9.12
Cuw + Cuf = Cu = 0.362fck bw xu + 0.447fck Df (bf -bw) =1450676.24 N.
Step 3: Eq.3.19
= 0.00247
Find fst:
From the table for Fe 415 steel we get:
| Strain | Stress |
| 0.00241 | 342.8 |
| 0.00247 | 344.44 |
| 0.00276 | 351.8 |
Tu = fst x Ast = 344.44 x 4310.27 =1484629.4 N.
We find that Cu in step 1 is not equal to Tu in step 4. So we have to do the process again. This time with an improved value of xu. This new improved value is obtained as follows:
(a) First find the value of xu as if the Tu obtained in the above cycle is the equilibrium force. So we can put Tu = 1484629.4 = Cu = 0.362fck bw xu + 0.447fck Df (bf -bw)
⇒ 1484629.4 = 2353xu + 871650
⇒ xu = 260.51 mm
(b) Now take the average of this value and the value of xu used in this cycle. Average value is equal to 0.5(260.51 + 246.08) = 253.3 mm. This average value is to be used as the trial value of xu in the next cycle.
Five cycles are done to complete the iteration process. It can be seen here. The first cycle that we did above, is also included in it. At the end of the fifth cycle, the value of xu obtained is 252.11 mm. We can use this value to calculate MuR.
Eq.9.11
= 509.45 kNm
This completes the analysis of the given beam section. In the next section we will see the analysis of another beam section.
PREVIOUS





No comments:
Post a Comment