In this section we will discuss about the arrangement of bars in the slab. Consider the fig.17.25 given below. It shows the bending moment diagrams in a two-way slab. This two-way slab that we are considering, is simply supported on all the four sides. The bending moment diagrams are shown in red color. The middle diagram is taller than the rest. This is the diagram for the middle strip. On either side of this strip, the diagrams are smaller, indicating that the strips on either side are carrying lesser bending moments. (If it was a one-way slab, all the diagrams would have been of the same height)
Fig.17.25
Bending moment diagrams for various strips in a two way slab

Bending moment diagrams for various strips in a two way slab

When we design the reinforcements, we provide steel for resisting Mu,x. This Mu,x, calculated using the coefficients from Table 26, is the maximum value at the middle of the middle strip. This value is indicated by the peak value in the above fig.17.25. But this value progressively becomes lesser as we move from the center towards the shorter sides. This is shown in the fig.17.26 given below:
Fig.17.26
Variation of peak value of Mu,x

Variation of peak value of Mu,x

The progressive reduction in the value of Mu,x is indicated by the green coloured graph. So the requirement of steel decreases as we move away from the center. At greater distances from the center, Mu,x may fall to such a low value that the steel required to resist this low value is less than even the minimum steel required for a slab. Obviously such low quantity of steel cannot be allowed to be provided. In the above fig.17.26, such regions are shown in yellow color. They are situated at a greater distance from the center. Also, at the middle regions where greater steel is required, it is not convenient to vary the spacing of bars from place to place, just to conform with the variation of Mu,x.
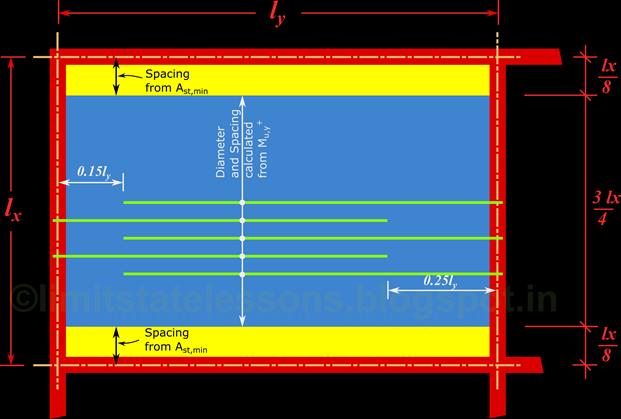
So we divide the slab into three segments. A larger middle portion AB and two smaller portions AD and BE on the sides. The diameter and spacing required to resist the maximum bending moment Mu,x is provided on the entire blue region AB. The yellow regions are provided with the minimum steel that is generally required for a slab. The measurements required for dividing the slab into these three strips is given by Cl. D-1 (fig.25) of the code. This is shown in the fig.17.27 below:
We can see that the middle strip (coloured in blue) has a width of 3/4 ly. The two strips on the sides (coloured in yellow) have a width of 1/8 ly. (1/8 + 3/4 + 1/8 = 1). For the whole width of the middle strip, the same diameter and spacing required for Mu,x should be provided. In the yellow portions, same diameter should be provided, but the spacing should be calculated using another method:
• Calculate the minimum steel required for slab. We know that this area should not be less than 0.0012Ag if Fe 415 steel is used, and 0.0015Ag if Fe 250 steel is used. This area is specified for unit width. So Ag = 1000 mm x D. Where D is the total depth of the slab. Details can be seen here.
• Calculate the spacing required from this minimum area.
• Calculate the minimum steel required for slab. We know that this area should not be less than 0.0012Ag if Fe 415 steel is used, and 0.0015Ag if Fe 250 steel is used. This area is specified for unit width. So Ag = 1000 mm x D. Where D is the total depth of the slab. Details can be seen here.
• Calculate the spacing required from this minimum area.
We made the above discussion based on fig.17.25 which show the bending moment diagrams for simply supported two-way slabs. The bending moment diagrams for continuous two-way slabs are also similar. They will have hogging moments at the supports. The variation of sagging moment Mu,x+ at midspan and Mu,x- at the supports is similar to that shown in fig.17.26. They will be maximum at midspan regions, and minimum near the shorter supports. So the division of slab area into three strips is applicable to continuous two-way slabs also.
The bars in the blue strip in fig.27 are to be provided parallel to lx. These bars extend from one long support to the other. But all the bars need not extend to the supports. Some of them can be curtailed. The distance at which bars can be curtailed are given in cl.D-1.4 of the code. According to this clause, the bars should extend upto a distance of 0.15lx from a simply supported edge and 0.25lx from a continuous edge. This is shown in the fig.12.28 below:
Technically, it is sufficient to show two bars belonging to a particular set of bars, in a drawing. But if more bars are shown, a definite pattern and symmetry in the arrangement of bars will become more clear. So 5 bottom bars are shown in the fig.12.28 above. We can see that all the bars which do not reach the continuous support has the same length, and all the bars which do not reach the simply supported edge has the same length. This is true for both the X and Y directions.
We have seen all the bottom bars in the X direction. The diameter and spacing for these bars are calculated from Mu,x+, and are laid parallel to lx. Also, they are laid as the bottom most layer.
Now we will see the bottom bars in the Y direction. Each of the above four figs. from fig.17.25 to 17.28 have a corresponding fig. in the Y direction. They are shown below from fig.17.29 to 17.32. They do not require much explanation, as they are similar to those in the X direction.
Fig.17.29
Bending moment diagrams in the Y direction for various strips in a two way slab

Bending moment diagrams in the Y direction for various strips in a two way slab

Fig.17.30
Variation of peak value of Mu,y

Variation of peak value of Mu,y

Fig.17.31
Division of slab area into three strips in the Y direction

Division of slab area into three strips in the Y direction

In the Y direction also we have two yellow strips. Just as in the X direction, we must provide the diameter and spacing required for the minimum steel in these yellow strips also. These bars are laid parallel to ly.
This completes the details of the bottom bars in the Y direction. The diameter and spacing for these bars are calculated from Mu,y+, and are laid parallel to ly. Also, they are laid just above the bottom most layer mentioned in fig.12.28.
So we have seen all the bottom bars in the two directions X and Y. They were shown separately in the above figs. just for clarity. In an actual problem, they must be shown in a single fig.
Copyright ©2015 limitstatelessons.blogspot.com - All Rights Reserved


No comments:
Post a Comment